زائر

تسجيل الاشتراك

لديك حساب؟ تسجيل دخول

  • ePub Logo
  • PDF Logo
  • Kindle Logo

ملاحظات ومراجع

مقدمة

(1)
Mars Odyssey, Mars Express, MRO, Mars Orbiter Mission, and MAVEN.
(2)
NASA’s Opportunity and Curiosity rovers. The Spirit rover ceased functioning in 2011.
(3)
‘This foolish idea of shooting at the Moon is an example of the absurd length to which vicious specialisation will carry scientists. To escape the Earth’s gravitation a projectile needs a velocity of 7 miles per second. The thermal energy at this speed is 15,180 calories [per gram]. Hence the proposition appears to be basically impossible.’ Alexander Bickerton, Chemistry Professor, 1926.
‘I am bold enough to say that a man-made Moon voyage will never occur regardless of all scientific advances.’ Lee De Forest, electronics inventor, 1957.
‘There is no hope for the fanciful idea of reaching the Moon because of insurmountable barriers to escaping the Earth’s gravity.’ Forest Moulton, astronomer, 1932.
(4)
In a 1920 editorial, the New York Times wrote: ‘Professor Goddard … does not know the relation of action to re-action, and the need to have something better than a vacuum against which to react.’ Newton’s third law of motion states that to every action there is an equal and opposite reaction. The reaction comes from conservation of momentum, and no medium to react against is required. Such a medium would impede progress, not assist it. To be fair, the newspaper apologised in 1969 when the Apollo 11 astronauts were on their way to the Moon. To every publication there is an equal and opposite retraction.
(5)
Nicolas Bourbaki is the pseudonym of an ever-changing group of mainly French mathematicians first formed in 1935, who wrote a long series of books reformulating mathematics on a general and abstract basis. This was great for research mathematics, because it unified the subject, sorted out basic concepts, and provided rigorous proofs. But the widespread adoption of a similar philosophy in the teaching of school mathematics, known as ‘new maths’ met with little success, and was, to say the least, controversial.

الفصل الأول: الجذب عن بُعد

(1)
In 1726 Newton spent an evening dining with William Stukeley in London. In a document preserved in the archives of the Royal Society, whose archaic spelling I’ve preserved for period flavour, Stukeley wrote:
“After dinner, the weather being warm, we went into the garden & drank thea under the shade of some apple tree; only he & myself. Amid other discourse, he told me, he was just in the same situation, as when formerly the notion of gravitation came into his mind. Why shd that apple always descend perpendicularly to the ground, thought he to himself; occasion’d by the fall of an apple, as he sat in contemplative mood. Why shd it not go sideways, or upwards? But constantly to the Earth’s centre? Assuredly the reason is, that the Earth draws it. There must be a drawing power in matter. And the sum of the drawing power in the matter of the Earth must be in the Earth’s centre, not in any side of the Earth. Therefore does this apple fall perpendicularly or towards the centre? If matter thus draws matter; it must be in proportion of its quantity. Therefore the apple draws the Earth, as well as the Earth draws the apple.”
Other sources also confirm that Newton told this story, but none of this proves the story true. Newton might have invented it to explain his ideas. A still extant tree – Flower of Kent, a cooking apple, at Woolsthorpe Manor – is said to be the one from which the apple fell.
(2)
If an ellipse has major radius a and minor radius b, then the focus lies at a distance from the centre. The eccentricity is .
(3)
A. Koyré. An unpublished letter of Robert Hooke to Isaac Newton, Isis 43 (1952) 312–337.
(4)
A. Chenciner and R. Montgomery. A remarkable periodic solution of the three-body problem in the case of equal masses, Ann. Math. 152 (2000) 881–901.
An animation, and further information about similar types of orbit, is at: http://www.scholarpedia.org/article/N-body_choreographies.
(5)
C. Simó. New families of solutions in N-body problems, Proc. European Congr. Math., Barcelona, 2000.
(6)
E. Oks. Stable conic-helical orbits of planets around binary stars: analytical results, Astrophys. J. 804 (2015) 106.
(7)
Newton put it this way in a letter to Richard Bentley, written in 1692 or 1693: “It is inconceivable that inanimate Matter should, without the Mediation of something else, which is not material, operate upon, and affect other matter without mutual Contact … That one body may act upon another at a distance thro’ a Vacuum, without the Mediation of any thing else … is to me so great an Absurdity that I believe no Man who has in philosophical Matters a competent Faculty of thinking can ever fall into it.”
(8)
That’s slightly simplistic. Passing through lightspeed is what’s forbidden. Nothing currently moving slower than light can speed up to become faster than light; if anything happens to be moving faster than light it can’t decelerate to become slower than light. Particles like this are called tachyons: they’re entirely hypothetical.
(9)
In a letter of 1907 to his friend Conrad Habicht, Einstein wrote that he was thinking about ‘a relativistic theory of the gravitational law with which I hope to account for the still unexplained secular change in the perihelion motion of Mercury’. His first significant attempts began in 1911.
(10)
Nowadays we combine Einstein’s equations into a single tensor equation (with ten components – a symmetric 4-tensor). But “field equations” remains the standard name.

الفصل الثاني: انهيار السديم الشمسي

(1)
The oldest minerals found in meteorites, modern traces of the first solid material in the pre-solar nebula, are 4.5682 billion years old.
(2)
He wrote it in 1662–3, but postponed publication because of the Inquisition. It appeared shortly after his death.
(3)
A proper definition requires vectors.
(4)
H. Levison, K. Kretke, and M. Duncan. Growing the gas-giant planets by the gradual accumulation of pebbles, Nature 524 (2015) 322–324.
(5)
I. Stewart. The second law of gravitics and the fourth law of thermodynamics, in From Complexity to Life (ed. N. H. Gregsen), Oxford University Press, 2003, pp. 114–150.
(6)
In this book the notation p:q for a resonance means that the first body mentioned goes round p times while the second goes round q times. Their periods are therefore in the ratio q/p. On the other hand their frequencies are in the ratio p/q. Some authors use the opposite convention; others use the notation “p/q resonance”. Reversing the order of the bodies turns a p:q resonance into a q:p resonance.
(7)
Venus doesn’t have old craters because its surface was reshaped by volcanism less than a hundred million years ago. The planets from Jupiter outwards are gas and ice giants, and all we can see is their upper atmosphere. But many of their moons have craters – some new, some old. New Horizons revealed that Pluto and its moon Charon have fewer craters than expected.
(8)
K. Batygin and G. Laughlin. On the dynamical stability of the solar system, Astrophys. J. 683 (2008) 1207–1216.
(9)
J. Laskar and M. Gastineau. Existence of collisional trajectories of Mercury, Mars and Venus with the Earth, Nature 459 (2009) 817–819.
(10)
G. Laughlin. Planetary science: The Solar System’s extended shelf life, Nature 459 (2009) 781–782.

الفصل الثالث: قمر متقلب

(1)
The chemistry of uranium deposits at Oklo, Gabon, suggests that in the Precambrian they constituted a natural fission reactor.
(2)
R. C. Paniello, J. M. D. Day, and F. Moynier. Zinc isotopic evidence for the origin of the Moon, Nature 490 (2012) 376–379.
(3)
A. G. W. Cameron and W. R. Ward. The origin of the Moon, Abstr. Lunar Planet. Sci. Conf. 7 (1976) 120–122.
(4)
W. Benz, W.L. Slattery, and A.G.W. Cameron. The origin of the moon and the single impact hypothesis I, Icarus 66 (1986) 515–535.
W. Benz, W.L. Slattery, and A.G.W. Cameron. The origin of the moon and the single impact hypothesis II, Icarus 71 (1987) 30–45.
W. Benz, A.G.W. Cameron, and H.J. Melosh. The origin of the moon and the single impact hypothesis III, Icarus 81 (1989) 113–131.
(5)
R. M. Canup and E. Asphaug. Origin of the Moon in a giant impact near the end of the Earth’s formation, Nature 412 (2001) 708–712.
(6)
A. Reufer, M. M. M. Meier, and W. Benz. A hit-and-run giant impact scenario, Icarus 221 (2012) 296–299.
(7)
J. Zhang, N. Dauphas, A.M. Davis, I. Leya, and A. Fedkin. The proto-Earth as a significant source of lunar material, Nature Geosci. 5 (2012) 251–255.
(8)
R. M. Canup, Simulations of a late lunar-forming impact, Icarus 168 (2004) 433–456.
(9)
A. Mastrobuono-Battisti, H. B. Perets, and S.N. Raymond. A primordial origin for the compositional similarity between the Earth and the Moon, Nature 520 (2015) 212–215.

الفصل الرابع: كون الساعة الآلية

(1)
See note 6 of Chapter 2 for why we don’t call it a 3:5 resonance.
(2)
Dermott’s law, an empirical formula for the orbital period of satellites in the solar system, was identified by Stanley Dermott in the 1960s. It takes the form , where n = 1, 2, 3, 4, … Here is the orbital period of the nth satellite, is a constant of the order of days, and C is a constant of the satellite system in question. Specific values are: Jupiter: = 0.444 days, C = 2.0. Saturn: = 0.462 days, C = 1.59. Uranus: = 0.488 days, C = 2.24.
S. F. Dermott. On the origin of commensurabilities in the solar system II: the orbital period relation, Mon. Not. RAS 141 (1968) 363–376.
S. F. Dermott. On the origin of commensurabilities in the solar system III: the resonant structure of the solar system, Mon. Not. RAS 142 (1969) 143–149.
(3)
F. Graner and B. Dubrulle. Titius-Bode laws in the solar system. Part I: Scale invariance explains everything, Astron. & Astrophys. 282 (1994) 262–268.
B. Dubrulle and F. Graner. Titius-Bode laws in the solar system. Part II: Build your own law from disk models, Astron. & Astrophys. 282 (1994) 269–276.
(4)
Derived from ‘QB1-0’, after (15760) 1992 QB1, the first TNO discovered.
(5)
It’s tricky to measure the diameter of Pluto from Earth, even using the Hubble telescope, because it has a thin atmosphere that makes its edges fuzzy. Eris has no atmosphere.
(6)
Propositions 43–45 of Book I of Philosophiae Naturalis Principia Mathematica.
(7)
A. J. Steffl, N. J. Cunningham, A. B. Shinn, and S. A. Stern. A search for Vulcanoids with the STEREO heliospheric imager, Icarus 233 (2013) 48–56.

الفصل الخامس: الشرطة السماوية

(1)
Wigner’s remark is often misunderstood. It’s easy to explain the effectiveness of mathematics. Much of it is motivated by real-world problems, so it’s no surprise when it solves those problems. The important word in Wigner’s phrase is “unreasonable”. He was referring to the way mathematics invented for one purpose often turns out to be useful in a totally different, unexpected area. Simple examples are Greek geometry of conic sections, turning up in planetary orbits two thousand years later, or Renaissance speculations about imaginary numbers, now central to mathematical physics and engineering. This widespread phenomenon can’t be explained away so easily.
(2)
Suppose, for simplicity, that all asteroids lie in the same plane – which isn’t too far from reality for most. The asteroid belt lies between 2.2 and 3.3 AU from the Sun, that is, about 320 million and 480 million kilometres. Projected into the plane of the ecliptic, the total area occupied by the asteroid belt is π(4802 − 3202) trillion square kilometres, that is, 4 × 1017 km2. Shared among 150 million rocks this gives an area of 8.2 × 108 km2 per rock. That’s the same area as a circle of diameter 58,000 km. If the asteroids are roughly uniformly distributed, which is good enough for government work, that’s the typical distance between neighbouring asteroids.
(3)
M. Moons and A. Morbidelli. Secular resonances inside meanmotion commensurabilities: the 4/1, 3/1, 5/2 and 7/3 cases, Icarus 114 (1995) 33–50.
M. Moons, A. Morbidelli, and F. Migliorini. Dynamical structure of the 2/1 commensurability with Jupiter and the origin of the resonant asteroids, Icarus 135 (1998) 458–468.
(4)
An animation showing the relationship between the five Lagrangian points and the gravitational potential is at https://en.wikipedia.org/wiki/File:Lagrangian_points_equipotential.gif.
(6)
F. A. Franklin. Hilda asteroids as possible probes of Jovian migration, Astron. J. 128 (2004) 1391–1406.

الفصل السادس: الكوكب الذي ابتلع أطفاله

(1)
P. Goldreich and S. Tremaine. Towards a theory for the Uranian rings, Nature 277 (1979) 97–99.
(2)
M. Kenworthy and E. Mamajek. Modeling giant extrasolar ring systems in eclipse and the case of J1407b: sculpting by exomoons? arXiv:1501.05652 (2015).
(3)
F. Braga-Rivas and 63 others. A ring system detected around Centaur (10199) Chariklo, Nature 508 (2014) 72–75.

الفصل السابع: نجوم كوزيمو

(1)
E. J. Rivera, G. Laughlin, R. P. Butler, S. S. Vogt, N. Haghighipour, and S. Meschiari. The Lick-Carnegie exoplanet survey: a Uranus-mass fourth planet for GJ 876 in an extrasolar Laplace configuration, Astrophys. J. 719 (2010) 890–899.
(2)
B. E. Schmidt, D. D. Blankenship, G. W. Patterson, and P. M. Schenk. Active formation of ‘chaos terrain’ over shallow subsurface water on Europa, Nature 479 (2011) 502–505.
(3)
P. C. Thomas, R. Tajeddine, M. S. Tiscareno, J. A. Burns, J. Joseph, T. J. Loredo, P. Helfenstein, and C. Porco. Enceladus’s measured physical libration requires a global subsurface ocean, Icarus (2015) in press; doi:10٫1016/j.icarus.2015.08.037.
(4)
S. Charnoz, J. Salmon, and A. Crida. The recent formation of Saturn’s moonlets from viscous spreading of the main rings, Nature 465 (2010) 752–754.

الفصل الثامن: رحلة على مذنَّب

(1)
M. Massironi and 58 others. Two independent and primitive envelopes of the bilobate nucleus of comet 67P, Nature 526 (2015) 402–405.
(2)
A. Bieler and 33 others. Abundant molecular oxygen in the coma of comet 67P/Churyumov–Gerasimenko, Nature 526 (2015) 678–681.
(3)
P. Ward and D. Brownlee. Rare Earth, Springer, New York, 2000.
(4)
J. Horner and B. W. Jones. Jupiter – friend or foe? I: The asteroids, Int. J. Astrobiol. 7 (2008) 251–261.

الفصل التاسع: الفوضى في الكون

(2)
J. R. Buchler, T. Serre, and Z. Kolláth. A chaotic pulsating star: the case of R Scuti, Phys. Rev. Lett. 73 (1995) 842–845.
(3)
Strictly, “dice” is the plural and “die” is the singular, but in language as she is actually spoke, almost everyone talks of “a dice”. I no longer see any point in fighting this, but I’m not using the word out of ignorance. I’m still fighting a rearguard action on usages such as “the team are”, but deep down I know I’ve lost that one too. I’ve also stopped trying to tell greengrocers the difference between the plural and the possessive, though I was sorely tempted to have a quiet chat with the bloke up the road whose van bears the sign: REMOVAL’S.
(4)
Nonetheless, a 6 has the same probability as any other value, for a fair dice. In the long run, the numbers of 6s should get arbitrarily close to 1/6 of the number of throws. But how this happens is instructive. If at some stage there have been, say, 100 more throws of a 6 than anything else, a 6 doesn’t become more likely. The dice just keeps churning out more and more numbers. After, say, a hundred million more throws, that extra 100 affects the proportion of 6s by only one part in a million. Deviations aren’t cancelled out because the dice “knows” it’s thrown too many 6s. They’re diluted by new data, generated by a dice that has no memory.
(5)
Dynamically, a dice is a solid cube, and its motion is chaotic because the edges and corners “stretch” the dynamics. But there’s another source of randomness in dice: initial conditions. How you hold the dice in your hand, and how you release it, randomise the result anyway.
(6)
Lorenz didn’t call it a butterfly, though he did say something similar about a seagull. Someone else came up with the butterfly for the title of a public lecture Lorenz gave in 1972. And what Lorenz originally had in mind probably wasn’t this butterfly effect, but a subtler one. See: T. Palmer. The real butterfly effect, Nonlinearity 27 (2014) R123–R141.
None of that affects this discussion, and what I’ve described is what we now mean by ‘butterfly effect’. It’s real, it’s characteristic of chaos, but it’s subtle.
(7)
V. Hoffmann, S. L. Grimm, B. Moore, and J. Stadel. Chaos in terrestrial planet formation, Mon. Not. RAS (2015); arXiv: 1508.00917.
(8)
A. Milani and P. Farinella. The age of the Veritas asteroid family deduced by chaotic chronology, Nature 370 (1994) 40–42.
(9)
June Barrow-Green. Poincaré and the Three Body Problem, American Mathematical Society, Providence, 1997.
(10)
M. R. Showalter and D. P. Hamilton. Resonant interactions and chaotic rotation of Pluto’s small moons, Nature 522 (2015) 45–49.
(11)
J. Wisdom, S. J. Peale, and F. Mignard. The chaotic rotation of Hyperion, Icarus 58 (1984) 137–152.
(12)
K = Kreide, German for ‘chalk’, referring to the Cretaceous, and T = Tertiary. Why do scientists do this kind of thing? Beats me.
(13)
M. A. Richards and nine others. Triggering of the largest Deccan eruptions by the Chicxulub impact, GSA Bull. (2015), doi: 10.1130/B31167.1.
(14)
W. F. Bottke, D. Vokrouhlický, and D. Nesvorný. An asteroid breakup 160 Myr ago as the probable source of the K/T impactor, Nature 449 (2007) 48–53.

الفصل العاشر: طريق ما بين الكواكب السريع

(1)
M. Minovitch. A method for determining interplanetary free-fall reconnaissance trajectories, JPL Tech. Memo. TM-312–130 (1961) 38–44.
(2)
M. Lo and S. Ross. SURFing the solar system: invariant manifolds and the dynamics of the solar system, JPL IOM 312/97, 1997.
M. Lo and S. Ross. The Lunar L1 gateway: portal to the stars and beyond, AIAA Space 2001 Conf., Albuquerque, 2001.
(3)
http://sci.esa.int/where_is_rosetta/ has a dramatic animation of this roundabout path.
(4)
One cause (among many) of World War I was the assassination of the Austrian Archduke Franz Ferdinand on a visit to Sarajevo. Six assassins made a failed attempt with a grenade. Later one of them, Gavrilo Princip, shot him dead with a pistol, along with his wife Sophie. Initial reaction by the populace was virtually non-existent, but the Austrian government encouraged rioting against Serbs in Sarajevo, which escalated.
(5)
W. S. Koon, M. W. Lo, J. E. Marsden, and S. D. Ross. The Genesis trajectory and heteroclinic connections, Astrodynamics 103 (1999) 2327–2343.

الفصل الحادي عشر: كرات عظيمة من النيران

(1)
Strictly speaking, this term refers to total energy output, but that’s closely related to intrinsic brightness.
(2)
An animation of stellar evolution across the Hertzsprung–Russell diagram can be found at http://spiff.rit.edu/classes/phys230/lectures/star_age/evol_hr.swf.
(3)
F. Hoyle. Synthesis of the elements from hydrogen, Mon. Not. RAS 106 (1946) 343–383.
(4)
E. M. Burbidge, G. R. Burbidge, W. A. Fowler, and F. Hoyle. Synthesis of the elements in stars, Rev. Mod. Phys. 29 (1957) 547–650.
(5)
A. J. Korn, F. Grundahl, O. Richard, P. S. Barklem, L. Mashonkina, R. Collet, N. Piskunov, and B. Gustafsson. A probable stellar solution to the cosmological lithium discrepancy, Nature 442 (2006) 657–659.
(6)
F. Hoyle. On nuclear reactions occurring in very hot stars: the synthesis of the elements between carbon and nickel, Astrophys. J. Suppl. 1 (1954) 121–146.
(7)
F. Hoyle. The universe: past and present reflections, Eng. & Sci. (November 1981) 8–12.
(8)
G. H. Miller and 12 others. Abrupt onset of the Little Ice Age triggered by volcanism and sustained by sea-ice/ocean feedbacks, Geophys. Res. Lett. 39 (2012) L02708.
(9)
H. W. Babcock. The topology of the Sun’s magnetic field and the 22-year cycle, Astrophys. J. 133 (1961) 572–587.
(10)
E. Nesme-Ribes, S. L. Baliunas, and D. Sokoloff. The stellar dynamo, Scientific American (August 1996) 30–36.
For mathematical details and more recent work with more realistic models, see: M. Proctor. Dynamo action and the Sun, EAS Publ. Ser. 21 (2006) 241–273.

الفصل الثاني عشر: نهر السماء العظيم

(1)
That is, . So . Here is the mass out to radius r, is the rotational velocity of stars at radius r, and G is the gravitational constant.

الفصل الثالث عشر: عوالم فضائية

(1)
X. Dumusque and 10 others. An Earth-mass planet orbiting α Centauri B, Nature 491 (2012) 207–211.
(2)
V. Rajpaul, S. Aigrain, and S. J. Roberts. Ghost in the time series: no planet for Alpha Cen B, arXiv:1510.05598; Mon. Not. RAS, in press.
(3)
Z. K. Berta-Thompson and 20 others. A rocky planet transiting a nearby low-mass star, Nature 527 (2015) 204–207.
(4)
“Earthlike” here means a rocky world, with much the same size and mass as the Earth, in an orbit that would allow water to exist as a liquid without any special extra conditions. Later we require oxygen as well.
(5)
E. Thommes, S. Matsumura, and F. Rasio. Gas disks to gas giants: Simulating the birth of planetary systems, Nature 321 (2008) 814–817.
(6)
M. Hippke and D. Angerhausen. A statistical search for a population of exo-Trojans in the Kepler dataset, ArXiv:1508.00427 (2015).
(7)
In Evolving the Alien Cohen and I propose that what really counts is extelligence: the ability of intelligent beings to pool their knowledge in a way that all can access. The Internet is an example. It takes extelligence to build starships.
(8)
M. Lachmann, M. E. J. Newman, and C. Moore. The physical limits of communication, Working paper 99–07–054, Santa Fe Institute 2000.
(9)
I. N. Stewart. Uninhabitable zone, Nature 524 (2015) 26.
(10)
P. S. Behroozi and M. Peeples. On the history and future of cosmic planet formation, Mon. Not. RAS (2015); arXiv: 1508.01202.
(11)
D. Sasselov and D. Valencia. Planets we could call home, Scientific American 303 (August 2010) 38–45.
(12)
S. A. Benner, A. Ricardo, and M. A. Carrigan. Is there a common chemical model for life in the universe? Current Opinion in Chemical Biology 8 (2004) 676–680.
(13)
J. Stevenson, J. Lunine, and P. Clancy. Membrane alternatives in worlds without oxygen: Creation of an azotosome, Science Advances 1 (2015) e1400067.
(14)
J. Cohen and I. Stewart. Evolving the Alien, Ebury Press, London, 2002.
(15)
W. Bains. Many chemistries could be used to build living systems, Astrobiology 4 (2004) 137–167.
(16)
J. von Neumann. Theory of Self-Reproducing Automata, University of Illinois Press, Urbana, 1966.

الفصل الرابع عشر: نجوم مظلمة

(1)
In units that make the speed of light equal to 1, say years for time and light years for space.
(2)
R. Penrose. Conformal treatment of infinity, in Relativity, Groups and Topology (ed. C. de Witt and B. de Witt), Gordon and Breach, New York, 1964, pp. 563–584; Gen. Rel. Grav. 43 (2011) 901–922.
(3)
Animations of what it would look like when passing through these wormholes can be found at http://jila.colorado.edu/~ajsh/insidebh/penrose.html.
(4)
B. L. Webster and P. Murdin. Cygnus X-1 – a spectroscopic binary with a heavy companion?, Nature 235 (1972) 37–38.
H. L. Shipman, Z. Yu, and Y. W. Du. The implausible history of triple star models for Cygnus X-1: Evidence for a black hole, Astrophys. Lett. 16 (1975) 9–12.
(5)
P. Mazur and E. Mottola. Gravitational condensate stars: An alternative to black holes, arXiv:gr-qc/0109035 (2001).

الفصل الخامس عشر: خصلات وفراغات

(1)
Colin Stuart. When worlds collide, New Scientist (24 October 2015) 30–33.
(2)
You may object that “currently” has no meaning because relativity implies that events need not occur simultaneously for all observers. That’s true, but when I say “currently” I’m referring to my frame of reference, with me as observer. I can conceptually set distant clocks by making changes of one year per light year; viewed from here, they will all be synchronised. More generally, observers in “comoving” frames experience simultaneity the way we would expect in classical physics.
(3)
N. J. Cornish, D. N. Spergel, and G. D. Starkman. Circles in the sky: finding topology with the microwave background radiation, Classical and Quantum Gravity 15 (1998) 2657–2670.
J. R. Weeks. Reconstructing the global topology of the universe from the cosmic microwave background, Classical and Quantum Gravity 15 (1998) 2599–2604.

الفصل السادس عشر: البيضة الكونية

(1)
Less than that! According to NASA it was 12% of a pixel.
(2)
Based on Type Ia supernovae, temperature fluctuations in the CMB, and the correlation function of galaxies, the universe has an estimated age of 13.798 ± 0.037 billion years. See Planck collaboration (numerous authors). Planck 2013 results XVI: Cosmological parameters, Astron. & Astrophys. 571 (2014); arXiv:1303.5076.
(3)
M. Alcubierre. The warp drive: hyper-fast travel within general relativity, Classical and Quantum Gravity 11 (1994). L73–L77.
S. Krasnikov. The quantum inequalities do not forbid spacetime shortcuts, Phys. Rev. D 67 (2003) 104013.
(4)
See Note 2 of Chapter 15 on simultaneity in a relativistic universe.

الفصل السابع عشر: الانتفاخ الكبير

(1)
The current figure for the temperature is 2.72548 ± 0.00057 K, see D. J. Fixsen. The temperature of the cosmic microwave background, Astrophys. J. 707 (2009) 916–920.
Other figures mentioned in the text are historical estimates, now obsolete.
(2)
This phrase is reused from Terry Pratchett, Ian Stewart, and Jack Cohen. The Science of Discworld IV: Judgement Day, Ebury, London, 2013.
(3)
Penrose’s work is reported in: Paul Davies. The Mind of God, Simon & Schuster, New York, 1992.
(4)
G. F. R. Ellis. Patchy solutions, Nature 452 (2008) 158–161.
G. F. R. Ellis. The universe seen at different scales, Phys. Lett. A 347 (2005) 38–46.
(5)
T. Buchert. Dark energy from structure: a status report, T. Gen. Rel. Grav. 40 (2008) 467–527.
(6)
J. Smoller and B. Temple. A one parameter family of expanding wave solutions of the Einstein equations that induces an anomalous acceleration into the standard model of cosmology, arXiv:0901.1639.
(7)
R. R. Caldwell. A gravitational puzzle, Phil. Trans. R. Soc. London A 369 (2011) 4998–5002.
(8)
R. Durrer. What do we really know about dark energy? Phil. Trans. R. Soc. London A 369 (2011) 5102–5114.
(9)
Marcus Chown. End of the beginning, New Scientist (2 July 2005) 30–35.
(10)
D. J. Fixsen. The temperature of the cosmic microwave background, Astrophys. J. 707 (2009) 916–920.
(11)
The stars in galaxies are bound together by gravity, which is thought to counteract the expansion.
(12)
S. Das, Quantum Raychaudhuri equation, Phys. Rev. D 89 (2014) 084068.
A. F. Ali and S. Das. Cosmology from quantum potential, Phys. Lett. B 741 (2015) 276–279.
(13)
Jan Conrad. Don’t cry wolf, Nature 523 (2015) 27–28.

الفصل الثامن عشر: الجانب المظلم

(1)
Quasi-autonomous non-governmental organisation.
(2)
K. N. Abazajian and E. Keeley. A bright gamma-ray galactic center excess and dark dwarfs: strong tension for dark matter annihilation despite Milky Way halo profile and diffuse emission uncertainties, arXiv: 1510.06424 (2015).
(3)
G. R. Ruchti and 28 others. The Gaia-ESO Survey: a quiescent Milky Way with no significant dark/stellar accreted disc, Mon. Not. RAS 450 (2015) 2874–2887.
(4)
S. Clark. Mystery of the missing matter, New Scientist (23 April 2011) 32–35.
G. Bertone, D. Hooper, and J. Silk. Particle dark matter: evidence, candidates and constraints, Phys. Rep. 405 (2005) 279–390.
(5)
Newton’s second law of motion is , where F = force, m = mass, a = acceleration. MOND replaces this by , where is a new fundamental constant that determines the acceleration below which Newton’s law ceases to apply. The term is an unspecified function that tends to 1 as x becomes large, in agreement with Newton’s law, but to x when x is small, which models observed galactic rotation curves.
(6)
J. D. Bekenstein, Relativistic gravitation theory for the modified Newtonian dynamics paradigm, Physical Review D 70 (2004) 083509.
(7)
D. Clowe, M. Bradač, A. H. Gonzalez, M. Markevitch, S. W. Randall, C. Jones, and D. Zaritsky. A direct empirical proof of the existence of dark matter, Astrophys. J. Lett. 648 (2006) L109.
(9)
S. Clark. Mystery of the missing matter, New Scientist (23 April 2011) 32–35.
(10)
J. M. Ripalda. Time reversal and negative energies in general relativity, arXiv: gr-qc/9906012 (1999).
(11)
See the papers listed at http://msp.warwick.ac.uk/~cpr/paradigm/.
(12)
D. G. Saari. Mathematics and the ‘dark matter’ puzzle, Am. Math. Mon. 122 (2015) 407–423.
(13)
The phrase “the exception proves the rule” is widely trotted out to dismiss awkward exceptions. I’ve never understood why people do this, other than as a debating ploy. It makes no sense. The word “prove” in that context originally had the meaning “test” – just as we still prove bread dough; that is, test to see if it’s the right consistency. (See en.wikipedia.org/wiki/Exception_that_proves_the_rule.) The phrase goes back to ancient Rome, in the legal principle exceptio probat regulam in casibus non exceptis (the exception confirms the rule in cases not excepted). Which means that if your rule has exceptions, you need a different rule. That does make sense. Modern usage omits the second half, producing nonsense.

الفصل التاسع عشر: خارج الكون

(1)
The truly fundamental constants are specific combinations of these quantities that don’t depend on the units of measurement: ‘dimensionless constants’ that are pure numbers. The fine structure constant is like that. The numerical value of the speed of light does depend on the units, but we know how to convert the number if we use different units. Nothing I say depends on this distinction.
(2)
B. Greene. The Hidden Reality, Knopf, New York, 2011.
(3)
What matters is that there’s some fixed number that’s bigger than the number of states of any patch. Exact equality isn’t required.
(4)
Numbers with huge exponents like these behave rather strangely. If you look on the web you’ll find that the nearest exact copy of you is about 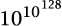metres away. I replaced that with light years, which are much bigger than metres. But actually, changing the units makes very little difference to the exponent, because 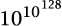metres is 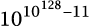light years, and the exponent 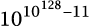is a 129-digit number, just like 10128. Their ratio is 1.000…00011 with 125 zeros.
(5)
B. Greene. The Hidden Reality, Knopf, New York, 2011, p. 154.
(6)
L. Carroll. The Hunting of the Snark, online free at https://www. gutenberg.org/files/13/13-h/13-h.htm.
(7)
G. F. R. Ellis. Does the multiverse really exist? Sci. Am. 305 (August 2011) 38–43.
(8)
O. Romero-Isart, M. L. Juan, R. Quidant, and J. I. Cirac. Toward quantum superposition of living organisms, New J. Phys. 12 (2010) 033015.
(9)
J. Foukzon, A. A. Potapov, and S. A. Podosenov. Schrödinger’s cat paradox resolution using GRW collapse model, Int. J. Recent Adv. Phys. 3 (2014) 17–30.
(10)
Known as a “ket” vector in Dirac’s formalism for quantum mechanics. The right-hand end of a bracket, OK? Mathematically, it’s a vector rather than a dual vector.
(11)
A. Bassi, K. Lochan, S. Satin, T. P. Singh, and H. Ulbricht. Models of wave-function collapse, underlying theories, and experimental tests, Rev. Mod. Phys. 85 (2013) 471.
(12)
J. Horgan. Physicist slams cosmic theory he helped conceive, Sci. Am. (1 December 2014); http://blogs.scientificamerican.com/cross-check/physicist-slams-cosmic-theory-he-helped-conceive/.
(13)
F. C. Adams. Stars in other universes: stellar structure with different fundamental constants, J. Cosmol. Astroparticle Phys. 08 (2008) 010.
(14)
V. Stenger. The Fallacy of Fine-Tuning, Prometheus, Amherst, 2011.
(15)
That is, on a log/log scale and in a specific but wide range of values, the region of parameter space for which stars can form has about one quarter the area of the whole space. This is a rough-and-ready measure, but it’s comparable to what fine-tuning proponents do. The point isn’t the 25%: it’s that any sensible calculation of the likelihood makes it far bigger than 1047−.

خاتمة

(1)
Adam G. Reiss and 14 others. A 2.4% determination of the local value of the Hubble constant, http://hubblesite.org/pubinfo/pdf/2016/17/pdf/pdf.
الرجوع إلى الصفحة الرئيسية للكتاب

جميع الحقوق محفوظة لمؤسسة هنداوي © ٢٠٢٤