الأنظمة الكوكبية
في عام ١٩٩٥، أعلن ميشيل مايور وديدييه كيلوز اكتشاف كوكب يدور حول النجم ٥١ بيجاسي، وهو نجم لا يختلف عن الشمس. منذ ذلك الحين، اكتُشِف نحو ١٠٠٠ نظام كوكبي خارج المجموعة الشمسية، ويُشكِّل فهم كيفية تكوُّن هذه الأنظمة وتطورها إلى حالتها الحالية أثرًا عميقًا في طريقة تفكيرنا في نظامنا الكوكبي، بل في مكاننا في الكون. يتطور فهمنا لتشكُّل النظم الكوكبية وتطوُّرها بسرعة، لكننا ما زلنا لا نعرف مدى تفرُّد نظامنا.
ديناميكا الأنظمة الكوكبية
| الكوكب | الاختلاف المركزي () | زاوية الميل () | الفترة | |||
|---|---|---|---|---|---|---|
| عطارد | ٠٫٠٥٥ | ٠٫٣٨٧ | ٠٫٢٠٦ | ٦٫٣٤ | ٠٫٢٤١ | ١ : ٤٩٫٢ |
| الزهرة | ٠٫٨١٥ | ٠٫٧٢٣ | ٠٫٠٠٧ | ٢٫١٩ | ٠٫٦١٥ | ١ : ١٩٫٣ |
| الأرض | ١ | ١ | ٠٫٠١٧ | ١٫٥٨ | ١ | ١ : ١١٫٩ |
| المريخ | ٠٫١٠٨ | ١٫٥٢٤ | ٠٫٠٩٣ | ١٫٦٧ | ١٫٨٨١ | ١ : ٦٫٣١ |
| المشتري | ٣١٧٫٨ | ٥٫٢٠٣ | ٠٫٠٤٩ | ٠٫٣٢ | ١١٫٨٦ | |
| زحل | ٩٥٫١٥ | ٩٫٥٨٢ | ٠٫٠٥٦ | ٠٫٩٣ | ٢٩٫٤٦ | ٢٫٤٨ : ١ |
| أورانوس | ١٤٫٥٤ | ١٩٫١٩ | ٠٫٠٤٧ | ١٫٠٢ | ٨٤٫٠٢ | ٧٫٠٨:١ |
| نبتون | ١٧٫١٥ | ٣٠٫٠٧ | ٠٫٠٠٩ | ٠٫٧٢ | ١٦٤٫٨ | ١٣٫٩ : ١ |
| بلوتو | ٠٫٠٠٢ | ٣٩٫٢٦ | ٠٫٢٤٥ | ١٧٫١ | ٢٤٧٫٧ | ٢٠٫٩ : ١ |
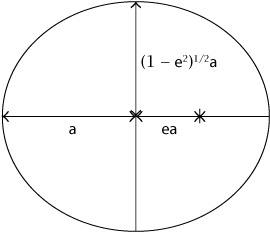
في اﻟ ٢٠ عامًا الأخيرة، أعادت تطوراتٌ جديدة الاهتمامَ بديناميكا الكواكب. أول هذه التطورات كان توفُّر أجهزة الكمبيوتر السريعة والرخيصة نسبيًّا، مما جعل من الممكن لأول مرة دمج المعادلات الكاملة للحركة عَبْر مليارات السنين، وثانيها كان اكتشاف الأنظمة الكوكبية خارج المجموعة الشمسية، التي هي في الغالب مختلفة اختلافًا كبيرًا عن نظامنا، مما دفع الفيزيائيين الفلكيين للتساؤل عن السبب في ذلك، وعما يمكن أن يخبرنا به عن النظام الشمسي.
الكواكب المضطربة
نظرًا لأن كتل الكواكب أصغر بكثيرٍ من كتلة الشمس، فإن النهج الطبيعي لدراسة ديناميكا الكواكب هو استخدام «نظرية الاضطراب»؛ حيث نضع الكواكب على مداراتها كما لو كانت جميعها عديمة الكتلة، ثم نسأل كيف سيتطور مدار كوكبٍ معين استجابةً للقوة المؤثِّرة فيه من الكواكب الأخرى. في هذا الإطار، يكون مدار الكوكب دائمًا أحد المدارات الإهليلجية لنيوتن حول الشمس، ولكن المدار يتغير تغيُّرًا بطيئًا استجابةً للاضطرابات الناجمة عن الكواكب الأخرى.
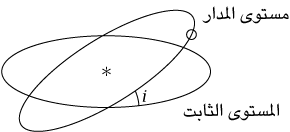
إذا كانت الكواكب ذات كتلةٍ ضئيلةٍ جدًّا، فإن اتجاه المحور الطويل لكل إهليلج كوكبي سيبقى ثابتًا في الفضاء. وإذا كان تأثير كتلة النظام الكوكبي مشابهًا لتأثير قرصٍ رقيق متماثل المحور من المادة في المستوى غير المتغير، فإن المحاور الطويلة للإهليلجات الكوكبية ستدور ببطء في الاتجاه المعاكس لدوران الكواكب حول إهليلجاتها. يُطلق على هذا الحركة العكسية للمحاور الطويلة اسم «المبادرة».

في هذا النموذج المحوري المتماثل للنظام الكوكبي، لكل كوكب تردُّد مبادرة خاص به. ونتيجةً لذلك، يتغير اتجاه عزم الدوران الذي يمارسه كوكب على آخر باستمرار؛ لأن الزاوية بين المحورَين الطويلَين لإهليلجي الكوكبَين تتغير مع مرور الوقت؛ بحيث ينتقل الزخم الزاوي من الكوكب الأول إلى الثاني بقَدْر ما ينتقله من الثاني إلى الأول. في ظل هذه الظروف، يتذبذب الاختلاف المركزي لمدار كل كوكب قليلًا، ولكن لا يحدث أي شيء أكثر إثارة للاهتمام. وعلى وجه الخصوص، تستمر الزاوية بين المحورَين الطويلَين لإهليلجي الكوكبَين في التزايد.
تُعدُّ حالات الرنين المشابهة للحالات الموصوفة للتو مفتاحًا لفهم العديد من الظواهر في أي فرع من فروع الفيزياء؛ حيث تكون الاضطرابات الصغيرة مؤثِّرة؛ لأن الاضطراب الصغير لا يصبح ذا أهمية إلا إذا استمرَّ في التأثير بالطريقة نفسها لفترة طويلة. في غياب الرنين، يتغير اتجاه الاضطراب باستمرار، مما يجعل تأثيره المتوسط زمنيًّا معدومًا، ولكن الرنين يمنح اضطرابًا ضعيفًا فرصة للعمل في الاتجاه نفسه لفترة طويلة، مما يؤدي إلى إحداث تغييرٍ كبير.
ولادة الكواكب
يُحيط بالنجم حديث العهد جدًّا بالتكوُّن قرص يُراكم المادة منه. ومع ازدياد كتلة النجم، ترتفع درجة الحرارة في لُبه (الفصل الثالث)، وإذا تجاوزَت كتلته ٠,٠٨ كتلة شمسية، تبدأ عمليات الاحتراق النووي داخله (الفصل الثالث). ومع ازدياد إضاءة النجم، تعمل إشعاعاته على تسخين القرص المحيط به، مما يؤدي إلى هروب الغاز الدافئ من مجال جاذبية النجم الشاب إلى الفضاء البينجمي. لكن جُسيمات الغبار في القرص تكون أكثر كتلة من أن تتمكن من الهروب، مما يؤدي إلى ارتفاع نسبة الغبار إلى الغاز في القرص مع استمرار تسخين النجم له. في هذا القرص المتزايد الغبارية، تتصادم جُسيمات الغبار وتندمج لتكوين جُسيمات أكبر. في النهاية، تصل بعض جُسيمات الغبار الأكثر ضخامة إلى أقطار تصل إلى عدة كيلومترات، مما يجعل مجالات جاذبيتها قوية بما يكفي لتغيير سرعات الغاز والغبار المحيط بها بشكلٍ ملحوظ. وهكذا تتكون «الكويكبات».
تتصادم الكويكبات تدريجيًّا وتندمج لتكوين كويكباتٍ أكبر فأكبر. وتؤدي الجاذبية الذاتية للكويكبات الضخمة إلى تشكيلها في أجرامٍ كرويةٍ منتظمة؛ حيث تستقر المواد الأكثر كثافة في المركز بينما ترتفع المواد الأقل كثافة إلى السطح. تُعرَف هذه الأجرام بالألباب الكوكبية.
إذا تشكَّل لُب ضخم مبكرًا، قبل أن يتلاشى الغاز عند نصف القطر، فقد يتمكن اللُّب من جذب بعض الغاز إلى مجال جاذبيته. بهذه الطريقة، تشكَّلَت الكواكب الخارجية العملاقة مثل المشتري، وزحل، وأورانوس، ونبتون، فيما لم تتمكن الكواكب الداخلية مثل عطارد، والزهرة، والأرض، والمريخ من اكتساب كمياتٍ كبيرة من الغاز؛ لأن مجالات جاذبيها لم تكن قوية بما يكفي للاحتفاظ بالهيدروجين والهيليوم في ظل درجات الحرارة المرتفعة السائدة في الجزء الداخلي من النظام الشمسي.
تطوُّر الأنظمة الكوكبية

عندما يفقد الجسم المداري زخمه الزاوي، فإنه يتحرك نحو الداخل. لذلك يتحرك الكوكب ببطء نحو النجم. وتتحرك المادة الموجودة خارج الحافة الداخلية للحلقة المُفرغة نحو الداخل أيضًا نتيجة فقدانها للزخم الزاوي لصالح الكويكب، ولكن ما دام الغاز متوفرًا بكثرة، تنقل اللزوجة الزخم الزاوي إلى الخارج عَبْر القرص بسرعةٍ كافيةٍ لتعويض الزخم الزاوي الذي فقده الكوكب. وبالمثل، خارج الحافة الخارجية للحلقة المُفرغة، تحمل اللزوجة الزخم الزاوي الذي يوفره الكويكب وتمنع الحافة الخارجية من التحرك نحو الخارج. وهكذا يتحرك الكوكب وحلقته المُفرغة ببطء نحو الداخل، «وفي عقبه» مادة القرص بحيث يبقى على اتصالٍ جاذبي جيد مع الكوكب على جانبَي الحلقة المُفرغة.
النظام الشمسي الشاب
يُعتقد أن كوكب زحل في فترة تكوُّنه المبكرة اصطدَم بالمشتري في فترة تكوُّنه المبكرة بالطريقة التي وصفناها، ودخل في حالة رنين متوسط الحركة بنسبة ٢ : ٣ مع المشتري (حيث تُعادل ثلاث سنوات على المشتري سنتَين على زحل)، ثم توقف الكوكبان عن الانجراف نحو الداخل بشكلٍ كبيرٍ بفضل عملهما المشترك. ثم جاء الكوكب التالي، الذي سنُسميه العملاق الجليدي الأول، وبتحركه نحو الداخل، واجه الزوج المشتري-زحل شبه الثابت، ودخل في حالة رنين متوسط الحركة على الأرجح أيضًا بنسبة ٢ : ٣ مع زحل، وأصبح النظام المكوَّن من ثلاثة كواكب مترابطة يتحرك ببطءٍ شديد في نصف القطر. ثم جاء الكوكب التالي، العملاق الجليدي الثاني، ودخل في حالة رنين متوسط الحركة مع العملاق الجليدي الأول. ربما بنسبة ٣ : ٤. وهكذا، بقيَت الكواكب الأربعة، بفضل عملها معًا، في أماكنها تقريبًا بينما كان النجم الشاب الشمس يبدِّد الغاز الموجود في القرص.
كان أحد العملاقَين الجليديَّين، ربما العملاق الجليدي الأول، يدور في مدار ذي اختلافٍ مركزي طفيف، وكان قادرًا على تبادل الطاقة والزخم الزاوي مع الكويكبات الموجودة بالقرب من الحافة الداخلية لحزام كايبر الأولي عند نصف قطر أصغر من ٢٠ وحدة فلكية. لو لم يكن مقيدًا برنين متوسطة الحركة مع الكواكب الأخرى، لكان قد استجاب لهذا الفقد بالانتقال إلى مدارٍ شبه دائري بنصف قطر أصغر. ولكن نظرًا لأنه كان مقيدًا، فقد استجاب بالانتقال إلى مدار ذي اختلافٍ مركزي أكبر. لفترة من الزمن، استمر اختلافه المركزي في التزايد تدريجيًّا، إلى أن تسبَّب فجأة رنينٌ علماني داخل النظام المكوَّن من أربعة كواكب في الاختلاف المركزي للعملاق الجليدي الأول، مما أدى إلى تغيير زخم الكواكب الزاوي بطريقة أدت إلى كسر شروط الرنين المتوسطة الحركة.
النظام والفوضى والكارثة
ترك لنا نيوتن أداةً رائعة للتنبؤ بالمستقبل، وهي المعادلات التفاضلية (الفصل الأول). باستخدام الأعداد التي تصف التكوين الحالي لنظامٍ ديناميكي كشروطٍ ابتدائية لحل المعادلة، يمكننا من خلال الحل استخراج توقعات لحالة النظام في أي وقت من الأوقات. ولكن للأسف، ظهر في القرن العشرين أن هذا النهج غالبًا ما يكون غير فعَّال. تكمن المشكلة في أن سلوك الحل يمكن أن يكون «شديد» الحساسية للشروط الابتدائية. اكتشف هنري بوانكاريه، ابن عم الرجل الذي قاد فرنسا خلال معظم الحرب العالمية الأولى (١٩١٤–١٩١٨)، هذه المشكلة في بداية القرن العشرين، ولكن لم تتضح أبعادها إلا في ستينيات القرن العشرين؛ إذ أصبح من الممكن حل المعادلات التفاضلية للأنظمة الديناميكية العامة باستخدام أجهزة الكمبيوتر الإلكترونية. يوفر النظام الشمسي مثالًا واضحًا ومذهلًا في الآن نفسه لهذه الظاهرة.
يمكن بسهولة كتابة المعادلات التفاضلية التي تحكم حركة الكواكب، كما أن الملاحظات الفلكية توفر شروطها الابتدائية بدقة عالية. ولكن هذه الدقة لا تتيح لنا التنبؤ بتكوين الكواكب إلا لنحو ٤٠ مليون سنة في المستقبل؛ وإذا تعدَّلَت الشروط الابتدائية ضمن حدود عدم اليقين في الملاحظات، فإن التنبؤات للفترات الزمنية بين ٥٠ و٦٠ مليون سنة لاحقة تختلف اختلافًا كبيرًا. للحصول على توقعات تمتد حتى ٦٠ مليون سنة بالدقة نفسها التي حصلنا عليها لتوقعات تمتد حتى ٤٠ مليون سنة، نحتاج إلى شروط ابتدائية أكثر دقة بمقدار ١٠٠ مرة، على سبيل المثال يجب معرفة المواقع الحالية للكواكب بهامش خطأ لا يتجاوز ١٥ مترًا. وإذا أردنا دقة مماثلة تمتد حتى ٦٠,١٥ مليون سنة، فعلينا معرفة مواقع الكواكب الحالية بهامش خطأ لا يتجاوز ١٥ مليمترًا. نحن هنا نواجه حدودًا صارمة لمعرفتنا؛ فمن غير المتصور أن نتمكن يومًا من تحديد التكوين الحالي للنظام الشمسي بدقة كافية تسمح لنا بالتنبؤ بمواقع الكواكب لأكثر من نحو ٦٠ مليون سنة في المستقبل. وهذا يمثل جزءًا ضئيلًا ومخيبًا للآمال من العمر الإجمالي للنظام الشمسي، الذي يبلغ ٤٦٠٠ مليون سنة.
في ظل هذه الظروف، كل ما يمكننا فعله هو استخدام المعادلات التفاضلية لحساب التكوينات الأكثر احتمالًا في المستقبل. ونفعل ذلك عَبْر أخذ عيناتٍ عشوائية من التكوينات الحالية التي تتفق مع البيانات الرصدية، ثم نحسب الحل المقابل لكل تكوينٍ مأخوذ لنتمكن من التنبؤ بمواقع الكواكب في كل حالة. التكوينات المستقبلية الأكثر احتمالًا هي تلك التي يمكن الوصول إليها عَبْر العديد من التكوينات الحالية المأخوذة كعيِّنات.
إحدى السمات المهمة لحلول المعادلات التفاضلية للنظام الشمسي هي أنه بعد تأرجح متغير معيَّن — مثل الاختلاف المركزي لعطارد — ضمن نطاقٍ ضيق لملايين السنين، فإنه يتحول فجأة إلى مدًى مختلف تمامًا. يعكس هذا السلوك أهمية الرنين في ديناميكا النظام؛ فعند نقطةٍ زمنية معيَّنة، تتحقق حالة رنينية تؤدي إلى تغيير تدفق الطاقة داخل النظام؛ إذ يمكن لاضطرابٍ صغير أن يتراكم على مدى آلاف أو ملايين الدورات ليؤدي إلى تأثيرٍ كبير. إذا بدأنا التكاملات من تكوين يختلف ولو قليلًا عن التكوين السابق، فقد لا تتحقق الحالة الرنينية، أو قد تتحقق في وقتٍ أبكر أو لاحق، مما يؤدي إلى حلولٍ مختلفة تمامًا.
أجرى لاسكار وجاستينو محاكاة لتطور النظام الشمسي من تكوينه الحالي باستخدام مجموعتَين من الحلول. في كل مجموعة، استخدما تكويناتٍ متوافقة مع أفضل البيانات الرصدية المتاحة كشرطٍ ابتدائي للحل. وقدَّرا مجموعةً من الحلول تمتد إلى خمسة مليارات سنة في المستقبل باستخدام نظرية نيوتن وحدها، بينما استخدما في المجموعة الأخرى تصحيحات أينشتاين الطفيفة. وقد وُجِد أنه عند إدراج تصحيحات أينشتاين، كان الاختلاف المركزي لعطارد أكبر من ٠,٧ في واحد في المائة فقط من الحلول، بينما في غياب هذه التصحيحات، كان هناك حل واحد فقط من بين ٢٥٠٠ حل أبقى عطارد في مدار باختلافٍ مركزي أقل من ٠٫٧. إذا وصل عطارد إلى اختلاف مركزي أكبر من ٠٫٧، فإن العواقب على الأرض ستكون كارثية؛ إذ سرعان ما يؤدي الاختلاف المركزي لعطارد إلى زيادة الاختلاف المركزي للزهرة، مما يؤدي إلى زيادة الاختلاف المركزي للأرض، الذي بدوره يؤدي إلى زيادة الاختلاف المركزي للمريخ. وتترتب على ذلك تداعياتٌ هائلة؛ فمن بين الحلول البالغ عددها ٢٥٠٠ للمعادلات النيوتنية غير المصحَّحة، اصطدم عطارد بالزهرة في ٨٦ حالة، واصطدم بالأرض في ٣٤ حالة. وحتى في الحالات التي لا تصطدم فيها الكواكب الداخلية ببعضها، فإنها إما تسقط في اتجاه الشمس أو تُقذف خارج النظام الشمسي تمامًا.
يبدو إذن أننا نعيش على حافة الهاوية، ولولا تصحيحات أينشتاين الطفيفة للغاية على معادلات نيوتن، لما كان كوكب الأرض على الأرجح قادرًا على توفير الملاذ لنا. وحتى مع تصحيحات أينشتاين، فإن استقرار كوكبنا غير مضمون إلا لفترة لا تتجاوز تقريبًا ٨٠ مليون سنة في المستقبل. على الرغم من ذلك، وبفضل النسبية العامة، فإن احتمال بقاء كوكب الأرض مرتفعٌ جدًّا حتى تبتلعه الشمس المتضخمة بعد حوالي أربعة مليارات سنة.
تجعل تصحيحات أينشتاين الحياة ممكنة من خلال تعطيل رنين ضعيف بين المشتري وعطارد. ونظرًا لضعف هذا الرنين، فإنه لا يؤثِّر على النظام إلا في ظل ظروف محدَّدة للغاية. وتصحيحات أينشتاين تجعل من الصعب تحقق هذه الظروف.
الأنظمة الكوكبية خارج المجموعة الشمسية
كان أول اكتشاف لا يشوبه اللبس لنظامٍ كوكبي خارج المجموعة الشمسية حديثًا نسبيًّا في عام ١٩٩٥ على يد ميشيل مايور وديدييه كيلوز، لكننا نعرف اليوم أكثر من ١٠٠٠ نظام كوكبي. يمكننا فهم تطوُّر الأنظمة الكوكبية من خلال تحليل إحصائيات تكويناتها المعروفة، وكأن الكون قد أجرى عددًا هائلًا من الحسابات لحلول معادلات التطور، التي يُفترض أنها دقيقة تمامًا.
لقد رأينا أن النظام الشمسي تمكَّن من الاحتفاظ بثمانية كواكب ذات مداراتٍ شبه دائرية رغم تعرضه لتهديدَين خطيرَين على الأقل، الأول وقع بعد ٧٠٠ مليون سنة من نشأته عندما فقدَت الكواكب العملاقة استقرارها المداري، والثاني لا يزال قائمًا اليوم؛ إذ إن أي تعديل طفيف في الفيزياء التي تحكم النظام الشمسي، حتى بمقدار جزء من ١٠٠ مليون، قد يؤدي إلى انهيار استقراره الداخلي.
لذلك، لم يكن مفاجئًا أن أولى الأنظمة التي أمكن اكتشافها كانت تشبه الحالة النهائية لإحدى هذه الكوارث؛ إذ تتكون من كوكبٍ مشابه للمشتري على مدار ذي اختلافٍ مركزي قصير نسبيًّا. ولكن ينبغي أخذ تأثيرات تقنيات الرصد في الاعتبار عند تفسير هذه النتائج، نظرًا لأن التقنية الرصدية المستخدَمة للعثور على هذه الأنظمة كانت منحازة انحيازًا كبيرًا لصالح اكتشاف الأنظمة التي تحتوي على كوكبٍ كبير في مدارٍ قصير؛ فقد اكتُشِفَت هذه الأنظمة من خلال مراقبة سرعات النجوم لرصد تغيرات السرعة الدورية التي تدل على دوران النجم حول مركز الكتلة المشترك بينه وبين كوكبه. فكلما كان الكوكب أكثر ضخامة وأقرب، زادت هذه التغيرات في السرعة؛ ومن ثَم زادت احتمالية رصدها وسط الضوضاء.
استُخدِمَت لاحقًا تقنيةٌ مختلفة تمامًا لاكتشاف الكواكب، وباستخدام هذه التقنية، أصبح من الممكن اكتشاف أنظمة تحتوي على عدة كواكب تدور في مداراتٍ شبه دائرية، وقد أمكن بالفعل اكتشاف مثل هذه الأنظمة. تعتمد هذه التقنية على مراقبة سطوع النجوم لرصد الانخفاض الطفيف في سطوعها عندما يمُر كوكب بين نجمه وكوكب الأرض. إلا أن هذه التقنية لا يمكنها سوى الكشف عن الأنظمة التي تُرصَد من زاوية حَدِّيَّة تقريبًا، كما أن جمع البيانات بالدقة المطلوبة لا يمكن تحقيقه إلا من الفضاء. في مايو ٢٠٠٩، أطلقَت ناسا القمر الاصطناعي كبلر لمراقبة النجوم في منطقةٍ صغيرة من السماء. وخلال السنوات الأربع التالية، تمكَّن كبلر من اكتشاف ما يقرب من ١٠٠٠ نظامٍ كوكبي، كما أعدَّ قائمة بعدة آلاف من النجوم التي أظهرَت مؤشراتٍ على وجود أنظمةٍ كوكبية. ولا يزال تقييم أهمية هذه البيانات مجالًا نشطًا للبحث العلمي.



