الفيزياء الفلكية النسبية
إن عالَم الفيزياء النيوتنية المألوف ليس سوى تقريب للفيزياء النسبية، وهو نهجٌ مريحٌ وفعَّال عندما تكون السرعات النسبية أصغر بكثير من سرعة الضوء. إلا أن علماء الفلك اكتشفوا العديد من الأجرام التي تتجاوز هذا القيد، مما يستوجب استخدام نظرية النسبية الكاملة لدراستها.
فيما يلي بعض الحالات التي يصبح فيها ضروريًّا استخدام نظرية النسبية.
- «المجرَّات الراديوية»: يُولِّد معظم الإشعاع الذي نرصده من المجرات الراديوية إلكترونات بمعامل لورنتز يساوي تقريبًا ١٠٥. تكون حركة هذه الإلكترونات الفائقة الطاقة في الغالب عشوائية، ولكن في لُب المجرة الراديوية غالبًا ما يُوجد نفاث بلازمي يتدفق بانتظام؛ حيث تكون الطاقة الحركية الكلية للبلازما أكبر بعدة مرات من طاقتها الكتلية الساكنة.
- «النجوم الزائفة المصغرة»: تُعتبر هذه الأجرام بمثابة نُسخ مصغرة من المجرَّات الراديوية؛ حيث يكون الثقب الأسود الذي يغذي النجم الزائف المصغر ذا كتلة تُعادل بضع كتل شمسية (الفصل الرابع)، في حين أن الثقب الأسود في المجرَّة الراديوية قد تصل كتلته إلى بضع مئات الملايين من الكتل الشمسية. يقلل تقليص الكتلة من الحجم الفيزيائي للظواهر، ويجعل تقلبها أكثر سرعةً، ولكنه لا يغير السرعات المميزة. ومن ثَم، فإن النسبية تُعد ذات أهميةٍ مماثلة لكلٍّ من النجم الزائف المصغر والمجرَّة الراديوية.
-
«أشعة جاما»: يُعتبر البوزيترون، وهو الجُسيم المضاد
للإلكترون، ظاهرةً نسبية أساسية، وقد تنبأ بوجوده
بي إيه إم ديراك أثناء محاولته التوفيق بين
ميكانيكا الكم والنسبية. عندما يفنَى إلكترون مع
بوزيترون، تتحول جميع طاقتهما إلى فوتونات، عادةً
فوتونَين. إذا كانت الإلكترونات غير نسبية (أي )، فإن كل فوتون يحمل طاقةً
تُعادل طاقة الكتلة الساكنة للإلكترون؛ أي ٥١١
كيلو إلكترون فولت
(keV). وقد
اكتشفَت التلسكوبات المخصَّصة لرصد أشعة جاما هذا
الخط الطيفي القادم من مركز مجرَّتنا، مما يشير
إلى وجود كثافةٍ كبيرة من البوزيترونات
هناك.
في عام ١٩٦٣، وقَّعَت المملكة المتحدة، والولايات المتحدة، والاتحاد السوفيتي معاهدةً تحظر إجراء اختباراتٍ للأسلحة النووية في الغلاف الجوي. وبسبب انعدام الثقة المتبادل، أطلقَت كلٌّ من الولايات المتحدة والاتحاد السوفيتي أقمارًا اصطناعية سرية مخصَّصة للكشف عن أشعة جاما الناتجة عن أي اختباراتٍ نووية غير معلَنة. ومما أثار دهشة الجميع أنه أمكن الكشف عن «العديد» من انفجارات أشعة جاما.
استمرَّت هذه الانفجارات فتراتٍ تتراوح بين بضع ثوانٍ ودقيقة، وكانت تحدث بوتيرةٍ متكررةٍ بكثرة، بحيث لا يمكن تفسيرها منطقيًّا على أنها ناتجة عن تفجيراتٍ نووية.
بعد أن عكف الخبراء العسكريون من كلا الجانبَين على تحليل البيانات سرًّا دون الوصول إلى تفسيرٍ واضح، علم كل طرف أن الطرف الآخر قد رصد الأحداث نفسها، وأصبح من الواضح أن مصادرها كانت فلكية. في عام ١٩٧٣، أُعلن عن البيانات للعامة، وحان الوقت ليشعر علماء الفلك بالحيرة. بدت الانفجارات موزَّعة بانتظام في جميع أنحاء السماء، مما يشير إلى أن مصادرها لم تكن مرتبطة بالنجوم في مجرَّتنا كما هي الحال مع معظم مصادر الأشعة السينية. وبدا أن المصادر إما أن تكون على مسافة تقارب ٠,١ كيلوفرسخ من الشمس، أو أن تكون منتشرة عَبْر حجم أكبر بكثير من مجرَّتنا. ولكن نظرًا لقصر المدة الزمنية لهذه المصادر، لم يكن ممكنًا ربطها بالمجرَّات النشطة، ولم يستطع أحد أن يفترض أن مصدرًا قريبًا من الشمس يمكن أن يكون مسئولًا عنها. في عام ١٩٨٦، تحلى بوهدان باتشينسكي بالجرأة لاقتراح أن هذه الانفجارات، رغم قصر مدتها الزمنية، «تقع» في مسافاتٍ كونية شاسعة، ومن المحتمل أن تكون مرتبطة بنوع من النجوم المتفجرة. وفي عام ١٩٩٧، تأكَّد هذا الافتراض عندما التقط تلسكوب ويليام هيرشل صورًا للمنطقة المحيطة بانفجار أمكن رصده حديثًا؛ حيث لوحظ «ضوء الغسق» المرئي المتلاشي بسرعة لهذا الحدث في مجرَّة بعيدة. منذ ذلك الحين، أصبح اكتشاف أضواء الشفق المرئية أمرًا روتينيًّا، وأمكن معرفة الأطياف المرئية للأجرام الأساسية المرتبطة بها. وقد أكَّدَت هذه البيانات أن العديد من انفجارات أشعة جاما مرتبطة بالفعل بنجومٍ متفجرة. كما أصبح واضحًا أن هناك أكثر من نوع من المصادر لانفجارات أشعة جاما، ولا يزال فهمنا لهذه الأجرام غير مكتمل. المؤكَّد أن النسبية تلعب دورًا جوهريًّا في فهم هذه الأجرام الفريدة.
-
«الأشعة الكونية»: تتعرض الأرض باستمرار لقصف من الجُسيمات
النسبية، ويُعد اكتشاف هذه الجُسيمات أقدم فرع من
فروع علم الفلك المرتبط بدراسة الظواهر ذات
الطاقات العالية. ولحسن الحظ، فإن معظم هذه
الجُسيمات الخطيرة تصطدم بذرات الأكسجين أو
النيتروجين في طبقات الغِلاف الجوي العليا. تتضرر
تلك النواة بشدة جرَّاء الاصطدام، وتتطاير
الشظايا إلى الأسفل، فتصطدم بنوًى أخرى في
طريقها. ومن ثَم، فإن جُسيمًا واحدًا شديد الطاقة
يمكنه، عند دخوله الغلاف الجوي، أن يولِّد
«وابلًا» من الأشعة الكونية.
تتنوع طاقات الجُسيمات التي تصطدم بالأرض، إلا أن عدد الجُسيمات المنخفضة الطاقة يفوق بكثيرٍ عدد الجُسيمات العالية الطاقة. فنادرًا ما تُرى الجُسيمات الأعلى طاقةً حتى بواسطة الكواشف التي تتميز بأكبر مساحات التجميع. غير أن الجُسيمات الأكثر طاقةً التي رُصِدَت حتى الآن تبلغ طاقتها حوالي ١٠٢٠ فولتات إلكترونية، فإذا كانت هذه الجُسيمات إلكترونات، فإن معامل لورنتز لها يبلغ نحو ١٠١٤، وإذا كانت بروتونات أو نيوترونات، فإنه يبلغ نحو ١٠١١. تتجاوز هذه الطاقات بكثير تلك التي تحقِّقها أقوى مُعجِّلات الجُسيمات؛ حيث يُعجِّل مصادم الهادرونات الكبير في جنيف حاليًّا البروتونات بمعامل لورنتز يبلغ نحو ١٠٣.
- «النجوم النيوترونية»: تبلغ سرعة الهروب من سطح النجم النيوتروني نحو ، مما يجعل هذه الأجرام نسبية بدرجة طفيفة فقط. لكنها تسمح بإجراء قياساتٍ دقيقة؛ ومن ثَم يمكن قياس التأثيرات النسبية المتواضعة بدقة وتوفير اختباراتٍ قوية لنظرية النسبية. يُعد النابض الثنائي هالس-تايلور (المعروف أيضًا باسم PSR B1913+16) أحد أكثر الأمثلة أهمية، وهو نظام يتكون من نجمَين نيوترونيَّين يدور كلٌّ منهما حول الآخر باختلافٍ مركزي ٠,٦٢ وزمنٍ دوري ٧,٧٥ ساعة. اكتشف هذا الثنائي جو تايلور وطالبه راسل هولس عام ١٩٧٤، وما زال يُرصَد بكثافة منذ ذلك الحين. رُصِد عددٌ قليل من الثنائيات النجمية النيوترونية المشابهة منذ ذلك الحين، لكن القيود التي تفرضها على نظرية النسبية أضعف؛ لأنها لم تُرصَد فتراتٍ طويلة حتى الآن.
- «مصادر الأشعة السينية»: رأينا في الفصل الرابع، أن أنصاف الأقطار الداخلية للأقراص التراكمية حول الثقوب السوداء تكون شديدة السخونة، لدرجة أن أقوى إشعاع لها يكون في صورة أشعةٍ سينية. هذه المناطق صغيرةٌ جدًّا لدرجة لا يمكن معها لتلسكوبات الأشعة السينية رؤيتها بوضوح، ولكن التأثيرات النسبية تُغيِّر أشكال خطوط انبعاث الأشعة السينية التي نرصدها.
- «النظام الشمسي»: تدور الأرض حول الشمس بسرعة تقارب ٣٠كم/ث-١ ونظرًا لأن هذه السرعة تساوي تقريبًا من سرعة الضوء، ولأن التأثيرات النسبية تكون عادةً أصغر من نظيراتها النيوتنية بعاملٍ تقريبي ، فمن المتوقع أن يكون تأثير النسبية على النظام الشمسي ضئيلًا جدًّا. ولكن نظرًا لأن النظام الشمسي يسمح بإجراء قياساتٍ دقيقة، فإن البيانات المرصودة تتطلب استخدام نظرية النسبية في تفسيرها، كما أنها توفِّر اختباراتٍ حاسمةً لصحة النظرية. علاوةً على ذلك، كما رأينا في الفصل الخامس، فإن ديناميكيات النظام الشمسي حساسة للغاية، وغياب التأثيرات النسبية كان سيؤدي إلى تكوينٍ مختلف جذريًّا للنظام الشمسي عما نراه اليوم.
- «الكون»: تُشكل المشكلات المفاهيمية عقبة أمام تطوير نموذجٍ مقنعٍ لديناميكيات الكون ضمن إطار الفيزياء النيوتنية. ومن ثَم فإن علم الكونيات لم يصبح فرعًا علميًّا متماسكًا ضمن علم الفيزياء إلا بفضل نظرية النسبية العامة لأينشتاين. في ستينيات القرن العشرين، أصبح علم الكونيات قائمًا على أسسٍ تجريبية قوية بفضل اكتشاف إشعاع الخلفية الكوني الميكروي، الذي يجعل بالإمكان دراسة الكون كما كان قبل ١٠٠ ألف سنة فقط من الانفجار العظيم، إلى جانب اكتشاف النجوم الزائفة، التي تقع غالبًا في مجرَّات تبعُد عنا بسرعاتٍ نسبية.
النسبية الخاصة
في الفصل الأول، أوضحتُ أن الفيزيائيين ملتزمون بمبدأ أن قوانين الطبيعة يجب أن تظل ثابتة في جميع الأماكن والأزمنة، وأي اختلاف في الظواهر المقيسة من مكان لآخر أو من زمن لآخر «يجب» أن يُعزى إلى تغير في الظروف التي تُطبَّق فيها القوانين الكونية. تنص نظرية النسبية الخاصة على متطلب جديد للَّاتغيُّر؛ حيث يجب أن تكون القوانين متطابقة في جميع المجرَّات، بغَض النظر عن سرعة تحرُّك بعضها بالنسبة إلى بعض، وكذلك في جميع المركَبات الفضائية، بغَض النظر عن سرعتها.
في عام ١٨٩٩، اكتشف هنريك لورنتز تماثلًا في معادلات ماكسويل للكهروديناميكا. يُطلق على هذا التماثل اليوم «تغايُر لورينتز»، ونعتبره مبدأً أساسيًّا في الفيزياء، لكن لورنتز لم يكن متأكدًا من الأهمية الفيزيائية لهذا التماثل الجديد. في عام ١٩٠٥، جادل أينشتاين بأن تماثل لورنتز يعكس حقيقة أن القوانين الكهرومغناطيسية تعمل بالطريقة نفسها على متن أي مركبة فضائية، بغَض النظر عن سرعتها. فاجأَت هذه الفكرة معاصري أينشتاين؛ لأن موجات ماكسويل الكهرومغناطيسية كان يُفترض أنها تنتشر في وسطٍ معيَّن، وهو «الأثير»، الذي لا يمكن أن يكون في حالة سكون بالنسبة إلى جميع المركَبات الفضائية. في الواقع، تتغير سرعة كوكب الأرض بنحو ٦٠كم/ث كل ستة أشهر، وكان من المفترض أن تكشف التجارب التي تعتمد على الضوء عن هذا التغيُّر. استغرب معاصرو أينشتاين عدم نجاح أي تجربة من هذا القبيل في الكشف عن حركتنا بالنسبة إلى الأثير حتى ذلك الحين. وقد جادل أينشتاين أنه، وبسبب تماثل لورنتز، يستحيل من حيث المبدأ اكتشاف الحركة بالنسبة إلى الأثير. يتميز هذا الوسط، الذي نُطلق عليه اليوم «الفراغ»، بخاصية مذهلة؛ حيث يبدو متطابقًا لجميع المراقبين، بغَض النظر عن حركة بعضهم بالنسبة إلى بعض. على وجه الخصوص، لا يمكن اعتبار أي مراقب في حالة سكونٍ مطلق، بل إن جميع الحركات نسبية بالنسبة إلى مراقبٍ آخر، ومن هنا جاء اسم نظرية أينشتاين.
وهي تقوم على مبدأ محير تمامًا، وهو أن الساعات المتحركة تعمل ببطء. على سبيل المثال، يقف بوب على رصيف المحطة ويراقب بدقة الساعة الموجودة في كمبيوتر أليس المحمول داخل القطار السريع أثناء مروره بسرعة. يستنتج بوب أن الساعة تعمل ببطء لأنها في حالة حركة. في المقابل، تُراقب أليس ساعة يد بوب وتستنتج أنها تعمل ببطء لأنها في حالة حركةٍ بالنسبة إليها. في الواقع، تعمل ساعة الكمبيوتر المحمول بدقة عندما تراقبها أليس، وبالمثل، تعمل ساعة اليد بدقة وفقًا لرؤية بوب، لكن كلتَيهما تبدوان وكأنهما تعملان ببطء عندما ينظر إليهما مراقبٌ متحرك. العامل الذي يتسبَّب في تباطؤ الساعات هو معامل لورنتز المرتبط بسرعة القطار.
أعمار الميونات
طاقة الكتلة الساكنة
وهكذا، فإن الراصدين على اختلافهم لا يتفقون حول الاتجاهات التي يتحرك فيها فوتونٌ ما. ثمَّة مثال يوضح فيزيائيًّا هذا الخلاف. في أحد أفلام الغرب الأمريكي الكلاسيكية، يطلق أحد الحراس على متن قطارٍ متحرك ينقل ذهبًا النار على قطاع الطرق. إذا أطلق الحارس رصاصته عموديًّا على العربة، فلن تتحرك الرصاصة عموديًّا على مسار القطار، لأن سرعتها داخل ماسورة المسدس تُضاف إلى الحركة الأمامية للقطار. لذا، إذا أراد الحارس إصابة هدف يقع بزاوية قائمة على مسار القطار عند موقعه الحالي، فعليه أن يوجِّه سلاحه إلى الخلف قليلًا من الموقع العمودي على العربة، وذلك كي تلغي سرعة الرصاصة في الماسورة الحركة الأمامية للقطار.
الآن، تخيَّل مجموعة من الحراس المذعورين على متن القطار يطلقون الرصاص عشوائيًّا في جميع الاتجاهات. في هذه الحالة، سيُطلَق نصف عدد الرصاصات للأمام بالنسبة إلى الاتجاه العمودي على العربة، بينما سيُطلق نصفها الآخر للخلف بالنسبة إلى الاتجاه العمودي على العربة. ومن ثَم عند الرصد من الأرض، سيتحرك أكثر من نصف الرصاص للأمام؛ لأن حركة القطار تؤدي إلى «التوجيه الأمامي» لوابل الرصاصات.
النفاثات
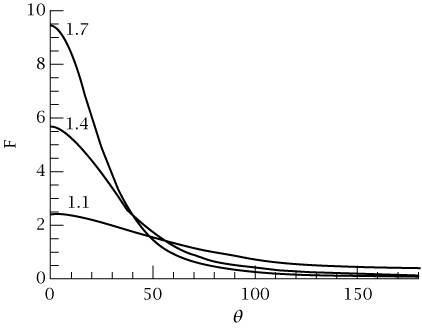
بوجهٍ عام، نتوقع أن يُصدر جِرمٌ مُعرَّض لتكوين النفاثات زوجًا من النفاثات المُتجِهة في اتجاهَين متعاكسَين. وعادةً، سيكون لأحد النفاثَين مكوِّن سرعة نحونا، وللآخر مكوِّن سرعة بعيدًا عنا. بسبب التوجيه الأمامي، سيكون النفاث المُقترِب أكثر سطوعًا من النفاث المُبتعِد. وبما أنه لا بد أن يتجاوز سطوع الجِرم سطوعًا حرِجًا ليُرى بأي شكل، فقد لا نتمكن سوى من رصد النفاث الآخِذ في الاقتراب. هذا الاحتمال وارد إذا تصادف أن نظرنا إلى الجِرم من مكانٍ قريب من الخط الذي تُطلَق النفاثات على طوله. أظهرَت العديد من المجرَّات الراديوية أن لها نفاثًا واحدًا فقط.
أحيانًا تُظهر النفاثات «حركة مفرِطة الإضاءة»، وهو أمر تمنعه النسبية. تحدث هذه الظاهرة عندما تُشاهَد بُقع داخل نفَّاث تتحرك عَبْر السماء بسرعةٍ تبدو أنها تتجاوز سرعة الضوء. تُقيَّم السرعة المعنية بافتراض أن البُقع تتحرك داخل مستوى السماء على أساس أن أي مكوِّن للسرعة عمودي على مستوى السماء لن يزيد سوى المسافة المقطوعة؛ ومن ثَم السرعة المُشتقَّة.
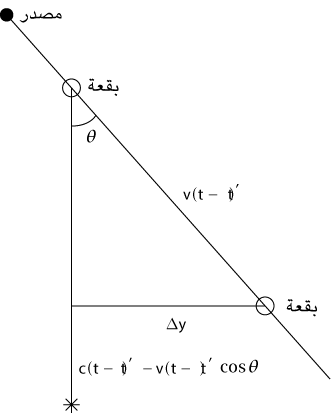
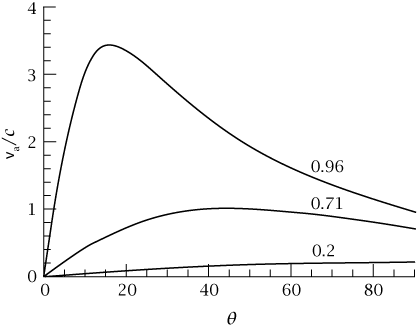
الصدمات وتسريع الجسيمات
الفضاء المحيط بجِرمٍ نسبي يطلق نفاثات لا يكون أبدًا فارغًا تمامًا. عندما ينبثق النفاث من المصدر، ربما تكون كثافته مرتفعة جدًّا لدرجة أن كثافة الوسط المحيط تصبح مهملة، ولكن مع ابتعاده عن المصدر، يتمدَّد جانبيًّا وتتناقص كثافته، مما يؤدي في النهاية إلى تأثيرٍ ملحوظٍ للوسط المحيط على النفاث.
أسهل طريقة لتصور ما يحدث عندما يشق النفاث طريقه في الوسط المحيط هي تخيُّل أنك تتحرك بسرعةٍ متوسطةٍ بين سرعة النفاث وسرعة الوسط المحيط. لنفترض أن النفاث يقترب من يسارك، وأن الوسط المحيط يقترب من يمينك. الفضاء الذي تقف فيه ممتلئ بمادة نشأَت نتيجة تصادم مادة النفاث مع مادة الوسط المحيط. هذه المادة شديدة السخونة؛ لأن الطاقة الحركية المنتظمة للنفاث القادم من اليسار، والمادة المحيطة القادمة من اليمين قد تحولتا إلى حركةٍ عشوائيةٍ سريعة ومضطربة لجُسيمات فردية، فالجُسيمات الفردية تتحرك بسرعةٍ كبيرة، ولكنها في المتوسط لا تتحرك في أي اتجاه؛ لذا فإن هذه «البلازما المصطدمة» تكون في حالة سكون بالنسبة إليك.
تتحرك منطقة البلازما الصدمية بعيدًا عن المصدر، وتزداد حجمًا باستمرارٍ نتيجة اصطدام المادة الجديدة المنبعثة من النفاث بها من اليسار، والمادة المحيطة بها من اليمين. يُطلَق على المناطق الضيقة التي يجري فيها تحويل الحركة المنتظمة لجُسيمات النفاث والوسط المحيط إلى حركةٍ عشوائيةٍ اسم «الصدمات».
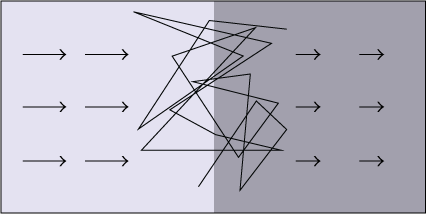
ينشأ هذا المجال في الأساس نتيجة فصل الإلكترونات عن الأيونات، وذلك نتيجة الفارق الهائل في الكتلة بينهما (بمقدار يزيد على ١٨٠٠ مرة)؛ فالإلكترونات القادمة تتباطأ قبل الأيونات الأكثر ضخامة بكثير، مما يؤدي إلى نشوء مناطق ذات كثافة شحنات موجبة وسالبة. هذه المناطق تُولِّد مجالًا كهربائيًّا يجذب الإلكترونات في اتجاهٍ معين والأيونات في الاتجاه المعاكس، مما يؤدي إلى تقارب سرعتها المتوسطة. تشير الفروقات في السرعات المتوسطة للإلكترونات والأيونات إلى وجود تياراتٍ كهربائية، التي بدورها تُولِّد مجالات مغناطيسية. علاوةً على ذلك، تكون تدفُّقات الإلكترونات والأيونات غير مستقرة للغاية في هذه المنطقة، مما يؤدي إلى تغيراتٍ زمنية في المجالات الكهربائية والمغناطيسية. ونظرًا لكون هذه المجالات متغيرة زمنيًّا، فإنها قادرة على تعديل طاقة الإلكترونات والأيونات الفردية، وفي المتوسط، تنقل الطاقة من الأيونات إلى الإلكترونات؛ ففي التدفق الأصلي والمنتظم قبل الصدمة، كان كلٌّ من الإلكترونات والأيونات يتحرك بالسرعة نفسها، مما يعني أن الطاقة الحركية للمادة كانت محصورةً في الغالب في الأيونات. أما بلازما ما بعد الصدمة «فتسترخي» إلى حالة من التوازن الحراري حيث يكون لكلٍّ من الإلكترونات والأيونات نصف الطاقة الحركية التي أصبحَت الآن عشوائية. يُعَد النقل الصافي للطاقة الحركية من الأيونات إلى الإلكترونات جزءًا أساسيًّا من هذه العملية الاسترخائية.
تُشبه البلازما الصدمية كازينو قمارٍ يجلب إليه المقامرون أموالهم التي يُعاد توزيعها داخل الكازينو. ناقشنا للتو كيف يؤثِّر هذا النقل على المقامر ذي المستوى المتوسط. ولكن بعض المقامرين يصبحون أثرياءَ للغاية نتيجة اكتسابهم للثروة في مرحلةٍ مبكرة.
في البلازما، يُعادل مفهوم الثروة الطاقة الحركية؛ فكلما تحرك الجُسيم بسرعة أكبر، زادت صعوبة انحرافه عن مساره. عندما يصل الجُسيم إلى سرعة كافية، يمكنه الإفلات تمامًا من المنطقة الصدمية؛ ومن ثَم الدخول إلى إحدى المنطقتَين على اليمين أو اليسار؛ حيث يكون التدفق منتظمًا. وبما أن هذه المناطق واسعة جدًّا، فإن الجُسيم «سوف» ينحرف إلى هناك، ثم يعود مرةً أخرى إلى المنطقة المتأثرة بالصدمة. ولكن عندما يعود، سيتحرك بسرعة أكبر من سرعته عند المغادرة، والسبب في ذلك هو أن انحرافاته في التدفق المنتظم أدَّت إلى عكس اتجاه سرعته «بالنسبة إلى التدفق». في الحالة غير النسبية، تصبح سرعته الجديدة هي مجموع سرعته الأصلية وسرعة المادة المتدفقة. وبما أن الجُسيم الآن يتحرك أسرع من أي وقتٍ مضى، فمن المحتمل أن يعبُر المنطقة الصدمية مباشرةً ويدخل إلى المنطقة المقابلة ذات التدفق المنتظم؛ حيث سينعكس اتجاه سرعته مجددًا بالنسبة إلى ذلك التدفق، وسيعود بسرعةٍ أكبر. من خلال هذه العملية، المعروفة باسم «تسارع فيرمي»، يمكن للجُسيمات اكتساب عوامل لورنتز كبيرة جدًّا. في الواقع، هكذا يمكن تسريع الأشعة الكونية التي نرصدها على الأرض.
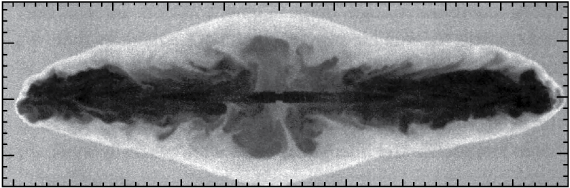
الإشعاع السنكروتروني
النسبية العامة
رأينا أن نظرية النسبية الخاصة نشأَت من معادلات ماكسويل في الكهروديناميكا، لكنها كشفَت عن تماثُلٍ أساسي في الزمكان. اقتنع أينشتاين بأن «جميع» القوانين الفيزيائية الأساسية يجب أن تعكس هذا التماثل، وكانت إحدى النظريات التي فشلَت في تحقيق ذلك على نحوٍ ملحوظ هي نظرية نيوتن للجاذبية.
هناك تشابهٌ وثيق للغاية بين الجاذبية والاستاتيكا الكهربائية؛ فمثل الجاذبية، تتناسب قوة الاستاتيكا الكهربائية مع معكوس مربع المسافة. أظهرَت نظرية النسبية أن المغناطيسية هي تعديل نسبي للاستاتيكا الكهربائية، بمعنى أن الراصد المتحرك يرى جزءًا من المجال الكهربائي كمجالٍ مغناطيسي؛ لذلك من المتوقع أن يبدو مجال الجاذبية مختلفًا للراصد المتحرك. على وجه الخصوص، يجب أن نتوقع أن تعتمد قوة الجاذبية الكاملة المؤثِّرة على جسمٍ ما على سرعته، تمامًا كما أن القوة الكهرومغناطيسية المؤثِّرة على شحنة لها مكوِّنٌ مغناطيسي يتناسب مع السرعة. وبما أن الفوتونات تتحرك أسرع من أي جُسيمٍ ذي كتلة سكون غير صفرية، فإن فهم هذا المكوِّن أمرٌ أساسي لفهم كيفية تأثير مجال الجاذبية على الفوتونات.
ثمَّة جانبٌ خاص للجاذبية لا يوجد في الاستاتيكا الكهربائية، وكان أينشتاين مقتنعًا بأهميته الجوهرية. هذا الجانب هو أن قوة الجاذبية تتناسب مع الكتلة. تقول الأسطورة إن جاليليو أثبت هذه الحقيقة نحو عام ١٦٠٠ بإسقاط كرتَين بوزنَين مختلفَين تمامًا من أعلى برج بيزا المائل، حيث وصلَت الكرتان إلى الأرض في اللحظة نفسها تقريبًا رغم اختلافهما في الوزن. لم تكن تجربة جاليليو دقيقة بدرجةٍ كبيرة. أُجري اختبارٌ أفضل بكثير لاعتماد قوة الجاذبية على الكتلة بقياس الفترات الزمنية لاهتزاز بندولاتٍ متساوية الطول، ولكن بكُرات ثِقلٍ مصنوعةٍ من موادَّ وكتلٍ مختلفة. في عام ١٨٩١، صمَّم البارون رولاند أوتفوش تجربة أظهرَت هذه التناسبية بدقةٍ عالية للغاية، من خلال دراسة التوازن بين انجذاب جسمٍ ما نحو الشمس والقوة المطلوبة للحفاظ عليه في مداره حولها. رأى أينشتاين أن مثل هذه التناسبية الدقيقة لا يمكن أن تكون مجرَّد مصادفة، بل لا بد أن تنبثق حتمًا من النظرية الصحيحة للجاذبية.
كافَح أينشتاين ١٠ سنواتٍ ليضع إطارًا رياضيًّا لهذا المفهوم، وأصبحَت نظريته الناتجة بلا شك واحدةً من أعظم الإنجازات الإبداعية في تاريخ البشرية. لقد فعل أينشتاين للجاذبية ما فعله ماكسويل للكهرومغناطيسية؛ حيث جمع عناصرَ فيزيائيةً متفرقة في بنيةٍ رياضيةٍ متماسكةٍ واحدة، لا تحتوي فقط على الفيزياء التي ألهمَتها، بل أيضًا على تنبؤات بظواهرَ جديدة كليًّا.
معادلات ماكسويل هي معادلاتٌ تفاضلية تُستخدَم في تحديد المجال الكهرومغناطيسي الناجم عن كثافةٍ معيَّنة من الشحنة الكهربائية والتيار الكهربائي، وبالمثل، فإن معادلات أينشتاين معادلاتٌ تفاضلية تُستخدَم في تحديد مجال الجاذبية الناجم عن كثافةٍ معيَّنة وتدفُّق معيَّن للطاقة-الزخم. إلا أن معادلات ماكسويل خطية، بينما معادلات أينشتاين «معادلات غير خطية»، وفي حالة المعادلات «الخطية»، يمكن حل المعادلة لإيجاد حلولٍ بسيطة، ثم تجميع هذه الحلول للحصول على حلولٍ أكثر تعقيدًا. أما في المعادلات غير الخطية، فإن مجموع حلَّين لا يُعطي بالضرورة حلًّا، مما يجعل بناءَ حلولٍ معقَّدة عَبْر جمعِ حلولٍ أبسط أمرًا غير ممكن.
نتيجةً لهذه المشكلة، فإن الحلول الدقيقة الوحيدة لمعادلات أينشتاين المتاحة حاليًّا هي تلك التي تتضمن تماثلاتٍ خاصة. أول وأشهر هذه الحلول هو الحل الذي قدَّمه كارل شفارتزشيلد عام ١٩١٦. يصف هذا الحل مجال الجاذبية حول كتلة كروية، وقد ناقشنا تطبيقه على النظام الشمسي في الفصل الخامس، تحت عنوان «الأنظمة الكوكبية خارج المجموعة الشمسية». في عام ١٩٦٣، عمَّم روي كير هذا الحل ليشمل مجال الجاذبية حول جِرمٍ دوَّار، وهو حلٌّ ذو أهميةٍ كبيرةٍ في فهم المناطق الداخلية للأقراص التراكمية (الفصل الرابع). وهناك حلولٌ دقيقة أخرى تصف نماذجَ كونيةً متماثلة. يمكن توسيعُ أيٍّ من هذه الحلول الدقيقة إلى حلٍّ تقريبي باستخدام نظرية الاضطراب (التي تطرَّقنا إليها في الفصل الخامس)، وتعتمد العديد من التطبيقات الفلكية للنسبية العامة على هذا النهج. منذ عام ٢٠٠٠، شهدَت الحلول العددية لمعادلات أينشتاين تقدمًا جوهريًّا. ويُعزى ذلك في جانبٍ منه إلى التطور المستمر في القدرة الحاسوبية، ولكن الأهم من ذلك هو التقدم في فهم كيفية التعامل مع هذه المعادلات.
الانزياح الأحمر الجذبوي
عدسة الجاذبية


يمكن لعلماء الفلك الاستفادة حتى من رداءة جودة عدسات الجاذبية. إذ تتمدد الصورة التي تتأثر بالتعدُّس الضعيف بشكلٍ متعامد مع اتجاه مجال الجاذبية. لذا، إذا شاهدنا مجموعةً من المجرات المستديرة في الأصل من خلال عدسة الجاذبية، فستبدو هذه المجرات إهليلجية الشكل. ستكون المحاور القصيرة لهذه القطوع الناقصة موازيةً للإسقاط السماوي لمجال الجاذبية، وستعكس نِسَب المحاور لهذه القطوع قوة المجال. يُعد استخدام هذه الفكرة لقياس مجالات الجاذبية أمرًا صعبًا من الناحية العملية، لا سيما بسبب الطبيعة الإهليلجية لصور المجرَّات. ولكن تشوُّه الصور بفعل مجال الجاذبية يؤدي إلى محاذاة القطوع الناقصة للمجرَّات المتقاربة في السماء، وقد أصبح القياس الدقيق لهذا التأثير أداةً رئيسيةً في علم الكونيات الحديث.
عدسة الجاذبية الصغرية
عندما يمُر نجمٌ في المقدمة أمام نجمٍ في الخلفية، قد يشكِّل مجال جاذبيته عدسةً قوية تعمل على تركيز ضوء النجم الخلفي. عادةً ما تتشكل صور النجم الخلفي بالقرب الشديد من بعضها لدرجة أن التلسكوبات الحالية لا يمكنها فصلها، لكن يمكن الاستدلال على تأثير العدسة من خلال طريقة سطوع النجم الخلفي مع تركيز مجال الجاذبية لضوئه نحو الأرض. يُعرف تكوين الصور المتعددة غير القابلة للفصل باسم «عدسة الجاذبية الصغرية»، ويُعد أداةً مهمةً لاستكشاف محتوى مجرَّتنا. في كثير من الحالات، يكون النجم في المقدمة خافتًا جدًّا بحيث لا نرى سوى نجمٍ واحدٍ يزداد سطوعه بزيادة مفاجئة ومؤقتة.
منذ أواخر تسعينيات القرن العشرين، يُرصَد سطوع مئات الملايين من النجوم كل ليلة، وتُكتشَف آلاف الحالات التي يحدث فيها تأثير عدسة الجاذبية الصغرية. لكن تفسير البيانات يظل مسألةً معقَّدة بسبب التغيرات في إضاءة العديد من النجوم. هناك طريقتان للتمييز بين هذه التغيرات وعدسة الجاذبية الصغرية: (١) عادةً ما تكون التغيرات الطبيعية مصحوبة بتغير في اللون، بينما لا يكون الحال كذلك في حالة تأثير عدسة الجاذبية الصغرية، (٢) من غير المرجَّح أن يخضع النجم لتأثير عدسة الجاذبية الصغرية أكثر من مرة عَبْر تاريخه، في حين أن النجم الذي يشهد تغيرًا في إضاءته من المرجَّح أن يشهده بشكلٍ متكرر.

انحراف الضوء بواسطة الشمس
عندما كانت نظرية أينشتاين لا تزال جديدة وغير مُختَبَرة، كان من غير الممكن رصد النجوم القريبة من الشمس إلا في أثناء الكسوف الشمسي. علاوةً على ذلك، كان القياس المطلوب بالغ الصعوبة؛ حيث إن الإزاحة المتوقَّعة في موضع النجم، حتى لو كان على حافة قرص الشمس، لا تتجاوز ١٫٧٥ ثانية قوسية، وجميع النجوم ضمن مجال رؤية صغير ستخضع لإزاحة مشابهة، مما يجعل قياس المواضع المطلقة للنجوم أكثر صعوبة بكثير من قياس الزوايا بين النجوم المجاورة. ولكن خلال كسوف عام ١٩١٩، قاس فريق بقيادة آرثر إدينجتون إزاحاتٍ متوافقةً مع تنبؤات أينشتاين.
يمكن من مركبةٍ فضائيةٍ رصد النجوم حتى بالقرب من الشمس، لكن التلسكوبات الفضائية تتجنب ذلك؛ لأن حسَّاساتها الدقيقة قد تتعرض للتلف الشديد إذا دخل أي جزء من قرص الشمس إلى مجال الرؤية عن طريق الخطأ. يتمتع القمر الاصطناعي جايا، الذي أُطلِق في ديسمبر ٢٠١٣، بدقة قياس فائقة للمواضع النجمية (أصغر بكثير من ٠٫٠٠٠٠١ ثانية قوسية) لدرجة أنه يجب أخذ تأثير إزاحة أينشتاين في الاعتبار عند قياس مواضع النجوم في السماء بأكملها. في الواقع، يتعين على التحليل أيضًا أن يأخذ في الحسبان انحراف الضوء بفعل الكواكب.
تأخيرات شابيرو
في ستينيات القرن العشرين، أصبح من الممكن ارتداد موجات الرادار عن الكواكب. كان الهدف هو قياس الزمن الذي تستغرقه النبضات للعودة إلى الأرض، ومقارنته بالزمن المتوقع وفقًا لنموذج النسبية العامة للنظام الشمسي. واجهَت هذه التجارب المبكرة مشكلتَين رئيسيتَين: (١) لا يحدث الانعكاس عن سطح الكوكب بشكل لحظي، بل يحدث على مدى فترة تعتمد على شكل الكوكب، و(٢) لا تنتقل الموجات الراديوية عَبْر الفضاء بين الكواكب بسرعة الضوء نفسها بالضبط، نظرًا لاحتواء الفضاء على طبقةٍ خفيفةٍ من البلازما تُغيِّر من معامل الانكسار عن القيمة واحد. يمكن تجاوز هاتَين المشكلتَين من خلال الاستعاضة عن الكواكب بمركباتٍ فضائيةٍ مبرمجة على إرسال إشارة استجابة بعد فترة تأخير معروفة بدقة، مما يسمح بقياس تأثير البلازما المتداخلة من خلال مقارنة النتائج باستخدام ترددات إرسال مختلفة، نظرًا لأن التأخير الناجم عن البلازما يعتمد على التردد.
تتيح هذه التجارب فحص مجال الجاذبية داخل النظام الشمسي مباشرة، والذي يُتوقَّع أن يكون شكلًا مضطربًا بدرجة طفيفة من حل كارل شفارتزشيلد لمعادلات أينشتاين. وقد أظهرَت النتائج أن أي فرق بين المجال الحقيقي والمتوقع يجب أن يكون أقل من جزء من الألف.
النجوم النابضة والموجات الثقالية
يمتلك العديد من النجوم النيوترونية، وربما جميعها، مجالاتٍ مغناطيسيةً تمتد منها، وتكتسح الفضاء المحيط أثناء دوران النجم النيوتروني. يمكن للمجال المغناطيسي الدوَّار أن يوِّلد حزمة من الموجات الراديوية التي تجوب الفضاء، على غرار الطريقة التي يمسح بها فانوس المنارة الدوَّار سطح المحيط. تسبِّب الفترات الدورية التي تمُر فيها هذه الحزمة عَبْر الأرض في إنتاج الإشارة الراديوية المميزة للنجم «النبَّاض».
يدور النجم النيوتروني بطريقةٍ منتظمةٍ للغاية؛ حيث يصعب على أي تأثيرٍ خارجي في بيئته أن يفرضَ عليه عزمَ دوران ملحوظًا. لذلك، يمكن إجراء قياساتٍ دقيقة عَبْر مقارنة الأوقات التي تُستقبَل فيها النبضات مع الأوقات التي يُتوقَّع أن تكون قد انبعثَت فيها، استنادًا إلى الدوران الثابت للنجم النيوتروني. أهم الأجرام من هذه الناحية هو النابض الثنائي هالس-تايلور (الوارد ذكره سابقًا في هذا الفصل). تتغير المسافة بين النجمَين بين ٠٫٧٥ و٣٫١٥ مليون كيلومتر (للمقارنة، يبلغ نصف قطر الشمس ٠٫٧٠ مليون كيلومتر). أحد النجمَين النيوترونيَّين نجم نباض، وتتنبأ النسبية العامة بنمط معقَّد جدًّا لأزمنة وصول نبضاته الراديوية؛ لأن المسافة التي تقطعها كل نبضة للوصول إلينا تتغير باستمرار، كما يتغير معامل الانكسار الفعَّال للفضاء الذي تعبُره النبضات أثناء مرورها عَبْر مجال الجاذبية المكثف للثنائي النجمي النيوتروني. وقد وُجد أن النمط المتوقع يتطابق تمامًا مع القياسات.
أيُّ نظرية للجاذبية تتسق مع التماثل الذي كشفَته تحويلات لورنتز ستتنبأ بأن النجم الثنائي يشع موجاتٍ ثقالية. في الواقع، عندما تتحرك مصادر مجال الجاذبية، يجري تحديث المجال ليتناسب مع المواقع الجديدة لهذه المصادر بشكلٍ أسرع بالقرب منها مقارنةً بالمناطق البعيدة، ويجري هذا التحديث من خلال موجات تنتشر في المجال انطلاقًا من المصادر المتحركة. تتبع فيزياء الإشعاع الأساسية للموجات الثقالية المبادئ نفسها التي تحكُم الموجات الكهرومغناطيسية؛ لذلك فإن العامل الأساسي للإشعاع الفعَّال هو أن يكون المصدر (الهوائي) ذا حجم لا يقل كثيرًا عن طول الموجة المنبعثة (كما تطرَّقنا في الفصل الثاني). وفي حالة النجم الثنائي، يعني هذا الشرط أن السرعات المدارية للنجوم يجب ألا تكون أقل بكثير من سرعة الضوء. ومن ثَم، فإن نجمَين نيوترونيَّين يكادان يتلامسان سيشعَّان الموجات الثقالية بكفاءةٍ عالية، ويفقدان الطاقة خلال فترة زمنية تُقدَّر بعددٍ قليل من الدورات المدارية (أجزاء من الثانية)، في المقابل فإن نظامًا ثنائيًّا بفاصل حوالي وحدة فلكية واحدة ومدة مدارية تبلغ سنة سيكون مشعًّا ضعيفًا للغاية للموجات الثقالية. من بين أفضل مصادر الإشعاع المعروفة لدينا هو النبَّاض هالس-تايلور. ولكنه ليس مصدرًا عاليَ الكفاءة؛ حيث إن الزمن المميز لفقدان طاقته عَبْر الإشعاع الثقالي يُقدَّر بنحو ٠٫٣ مليون سنة؛ أي ما يعادل نحو ٣٤٠ مليون دورة مدارية. غير أن دقة قياسات توقيت وصول النبضات كانت كافيةً للكشف عن التغير في الفترة المدارية الناتج عن الإشعاع الثقالي، الذي وُجد أنه يتفق على نحوٍ مذهلٍ مع تنبؤات نظرية أينشتاين.
في وقت كتابة هذه السطور، لم تكن قد رُصدَت بعدُ الموجات الثقالية، وذلك لأن بناءَ هوائيٍّ فعَّالٍ يُعدُّ مهمةً بالغةَ الصعوبة؛ إذ يتطلب الأمر أجرامًا ضخمة تتحرك بسرعاتٍ قريبةٍ من سرعة الضوء. يجري تطوير كاشفاتٍ متقدمة تعتمد على تمرير الضوء ذهابًا وإيابًا داخل نفقَين مفرغَين بطول خمسة كيلومترات، يتعامد كلٌّ منهما على الآخَر. تُرصد أهداب التداخل بين الضوء الذي انتقل عَبْر أحد الأنفاق والضوء الذي سلك النفق الآخر. وعند مرور موجةٍ ثقاليةٍ عَبْر النظام، فإنها تغير مُعامل الانكسار الفعَّال داخل الأنفاق، مما يؤدي إلى انزياح أهداب التداخل. التأثير المتوقع لأي مصدر فلكي ضئيل للغاية، لكنه من المفترض أن يُرصَد خلال بضع سنوات. سيُعدُّ هذا الإنجاز واحدًا من أصعب التحديات في تاريخ الفيزياء التجريبية.



