معادلات القضايا وأخطاء المنطق التقليدي
نقول عن القضيتين إنهما متعادلتان أو متساويتان، لو كان بينهما تطابُق ذاتي، أعني لو أمكن للواحدة أن تحل مكان الأخرى دون أن يتغير الموقف من حيث الصدق أو الكذب.
ويجمل بنا أن نذكر قائمة بالرموز المستعملة في حساب القضايا، هي شبيهة إلى حد كبير بالرموز المستعملة في حساب الحدود، حتى يرجع إليها القارئ فيما نحن ذاكروه له بعد ذلك من معادلات.
-
(١)
سنرمز للقضايا بالرموز «ق» و«ك» و«ل» … إلخ، أي إنك إذا وجدت عبارة كهذه: «ق» يلزم عنها «ك» فاعلم أن كلًّا من الرمزَين «ق» و«ك» يرمز إلى قضية بأسرها، لا إلى حد واحد.
-
(٢)
سنرمز إلى القضية السالبة بعلامة النفي «~»، فلو كتبنا صيغة كهذه: «~ ق» كان معناها «نقيض القضية ق» أو «القضية ق كاذبة»، على اعتبار أن مجرد ذكرنا لرمز القضية «ق» معناه «ق صادقة» حتى لو لم نَصِفْها بالصدق صراحةً، وإذَن فنقيضها «~ ق» يكون معناه كما قلنا «ق كاذبة».
-
(٣)
سنرمز لعلاقة اللزوم أو التضمن، بالرمز «⊂»، فإذا وجدنا صيغة كهذه: «ق ⊂ ك» كان معناها: «إذا كانت القضية ق صادقة، إذَن فالقضية ك صادقة كذلك» أو بعبارة أخرى «القضية ق تلزم عنها القضية ك» أو بعبارة ثالثة «القضية ق تتضمَّن القضية ك».
-
(٤)
سنرمز لعلامة البدائل بين قضيتين، أعني للعلاقة التي نعبر عنها بكلمة «أو»، بالرمز «∨» [بدلًا من علامة + التي استعملناها لهذا المعنى في معادلات الحدود].فإذا كتبنا صيغة كهذه: «ق ∨ ك» كان معناها «إما ق أو ك» وبعبارة أخرى «إحدى القضيتين «ق» و«ك» على الأقل صادقة» (وقد تكونان صادقتين معًا، لأن هذا هو معنى «أو» في المنطق).
-
(٥)
سنرمز لعلامة التساوي بين قضيتين بالرمز «≡» [بدلًا من الرمز «=» الذي استعملناه ليدل على التساوي بين الحدود].فإذا كتبنا صيغة كهذه: «ق ≡ ك» كان معناها أن قضية «ق» معادلة لقضية «ك» أو بعبارة أخرى «قضيتا ق، ك» صادقتان معًا أو كاذبتان معًا.
على أنك قد تجد التعادل بين القضايا يُرمَز له أيضًا بعلامة التساوي المألوفة «=» في بعض الحالات، عند مَن كتبوا في المنطق الرمزي.
-
(٦)
سنستعمل الرمز «:» ليدل على أن مجموعة الرموز التي على يمينه أو على يساره، تؤخذ وحدة واحدة، وبذلك يقوم هذا الرمز مقام الأقواس؛ فإذا أردنا وضع قوسين داخل قوسين استعملنا رمز النقطتين «:» ليقوم مقام القوسين الكبيرين، ورمز النقطة الواحدة يقوم مقام القوسين الصغيرين، فهذه الصيغة [(ق ≡ ك) و(ك ≡ ل)] ⊂ (ق ≡ ل) تُكتَب هكذا بعد رفع الأقواس ووضع رموز النقط مكانها ق ≡ ك ⋅ ك ≡ ل: ⊂ ⋅ ق ≡ ل.
-
(٧)
سيكون معنى النقطة الواحدة «⋅» أداة عطف تعطف قضيتين، أو صيغتين إحداهما على الأخرى.
-
(٨)
يدل الرقم «١» إذا عادلنا بينه وبين قضية ما، على أن القضية صادقة دائمًا، والرقم «صفر» إذا عادلنا بينه وبين قضية ما، على أن القضية كاذبة دائمًا؛ فهذه الصيغة «ق ≡ ١» معناها أن القضية ق صادقة دائمًا، وهذه الصيغة «ك ≡ صفر» معناها أن القضية «ك» كاذبة دائمًا.لما كنا قد أسلفنا [في ٢] أن رمز القضية مسبوقًا بعلامة النفي ~ مثل «~ ك» معناها أن القضية كاذبة، وأن مجرد ذكر رمز القضية بغير وصف يدل على أن القضية صادقة، فإن الصيغتين «ك = صفر» و«~ ك» تكونان متعادلتين، وكذلك الصيغتان «ق» و«ق = ١» متعادلتان.
وسنذكر الآن أمثلة تطبيقية نستخدم فيها الرموز السابقة مع توضيح معناها، تعويدًا للقارئ على استعمالها وفهمها.
تقرأ هذه الصيغة هكذا: قولنا إن القضية «ق» تساوي صفرًا، مطابق لقولنا إن القضية «ق» كاذبة.
وتقرأ هذه الصيغة كما يأتي: كون القضية ق تلزم عنها القضية ك، وكون القضية ك تلزم عنها القضية ل، كل ذلك يلزم عنه أن القضية ق تلزم عنها القضية ل.
ومعنى هذه الصيغة باللفظ هو ما يأتي: قولنا عن قضيتين «ق» و«ك» إنهما متطابقتان في الصدق، مساوٍ لقولنا عنهما إنهم كذلك متطابقتان في الكذب.
(١) قصة «التقابل» بين القضايا الأربع التقليدية
حدثناك في الفصل السادس عن القضايا الأربع التقليدية: الموجبة الكلية، والسالبة الكلية والموجبة الجزئية، والسالبة الجزئية باسطين في ذلك وجهة النظر الجديدة، التي مؤداها أن هذه «القضايا» المزعومة ليست بقضايا على الإطلاق، وإنما هي دالات قضايا؛ ولهذه التفرقة الخطيرة أثرها البعيد في وصف الكلام بالصدق أو بالكذب — وهو من أهم ما يهتم له المنطق — إذ إن القضية الكلية (موجبة أو سالبة) والقضية الجزئية (موجبة أو سالبة) لا يمكن وصفها بصدق أو بكذب إلا إذا حولناهما إلى قضايا تتحدث عن أفراد معينة، كما سنرى بعد قليل.
وما دمنا نتحدث في هذا الفصل عن معادلات القضايا في المنطق الرمزي، فيحسن قبل المضي في بسط الكلام عن القضايا الأربع التقليدية وما بينها من تقابل في المنطق الأرسطي، أن نضع تلك القضايا التقليدية الأربع في صورة معادلات رمزية لكي تستقر في الذهن صورة صحيحة تعاون على تتبع ما نقوله عنها.
-
(١)
فالقضية الموجبة الكلية: «كل أ هي ب» تكتب في المنطق الرمزي كما يأتي:
أ ⊂ ب وبالتالي أ ~ ب = صفرومعنى الصيغة الأولى هو: كل فرد من أفراد الفئة «أ» داخل في أفراد الفئة «ب» أو بعبارة أخرى، كل ما يوصف بأنه «أ» يوصف كذلك بأنه «ب».
ومعنى الصيغة الثانية المساوية لها، هو: أن اجتماع صفتي «أ» و«لا − ب» في شيء واحد لا وجود له، أي إن الفئة التي تجتمع في أفرادها صفتا «أ» و«لا − ب» فئة فارغة بغير أفراد؛ بعبارة ثالثة، لا وجود لفرد تستطيع أن تدخله في فئة «أ» وفي فئة «لا − ب» في آن معًا لأن كل فرد يدخل في فئة «أ» تراه يدخل في الوقت نفسه في فئة «ب».
-
(٢)
والقضية السالبة الكلية «لا أ هي ب» تكتب في المنطق الرمزي كما يأتي:
أ ~ ⊂ ب وبالتالي أ ب = صفرومعنى الصيغة الأولى هو أن كل فرد داخل في فئة «أ» لا بد أن يكون خارجًا عن فئة «ب» فكون الشيء موصوفًا بأنه «أ» يقتضي أن يكون موصوفًا بأنه «ليس ب».
ومعنى الصيغة الثانية هو أن صفتي «أ» و«ب» لا تجتمعان في فرد واحد أي أن الفئة التي أفرادها «أ» و«ب» معًا فئة فارغة بغير أفراد، بعبارة أخرى لا جود لفرد تستطيع أن تدخله في فئتي «أ» و«ب» في آن واحد.
-
(٣)
والقضية الموجبة الجزئية «بعض أ هي ب» تكتب في المنطق الرمزي هكذا:
أ ب ≠ صفرومعناها أن الأفراد التي تدخل في فئتي «أ» و«ب» معًا ليست معدومة الوجود، أو بعبارة أخرى: هنالك على الأقل فرد واحد موجود فعلًا تجتمع فيه صفتا «أ» و«ب» معًا.
-
(٤)
والقضية السالبة الجزئية «بعض أ ليس ب» تكتب في المنطق الرمزي هكذا:
أ ~ ب ≠ صفرومعناها أن الأفراد التي تدخل في فئة «أ» وتكون خارجة عن فئة «ب» ليست معدومة الوجود، أو بعبارة أخرى: هنالك على الأقل فرد أ واحد موجود فعلًا يدخل في فئة «أ» ولا يدخل في فئة «ب».
- (١) الموجبة الكلية رمزها أ ~ ب = صفر
- (٢)
السالبة الكلية رمزها أ ب = صفر
- (٣) الموجبة الجزئية رمزها أ ب ≠ صفر
- (٤) السالبة الجزئية هي أ ب ≠ صفر
هذه معادلات أربع، الشطر الأيسر في كل منها هو صفر، ولذلك فالمقارنة بينها واضحة.
فواضح أن الأولى والرابعة نقيضان، وهما الموجبة الكلية والسالبة الجزئية، إذ ترى في الأولى أن اجتماع «أ» و«لا − ب» يساوي صفرًا بينما ترى في الثانية أن اجتماعهما لا يساوي صفرًا.
وواضح أيضًا أن الثانية والثالثة نقيضان، وهما السالبة الكلية والموجبة الجزئية؛ إذ ترى في الأولى أن اجتماع «أ» و«ب» يساوي صفرًا، بينما ترى في الثانية أن اجتماعهما لا يساوي صفرًا.
وواضح كذلك من هذه المعادلات الأربع، أن الكليتين الموجبة والسالبة (وهما المعادلتان الأولى والثانية) تقولان إن شيئًا ما يساوي صفرًا، أي إن شيئًا ما لا وجود له، ففي حالة الموجبة الكلية، اجتماع «أ» و«لا − ب» في فرد ما، لا وجود له، وفي حالة السالبة الكلية، اجتماع «أ» و«ب» في فرد ما، لا وجود له.
وأما الجزئيتان الموجبة والسالبة (وهما المعادلتان الثالثة والرابعة) فتقولان إن شيئًا ما ليس صفرًا، أي إن شيئًا ما ليس معدوم الوجود، ففي حالة الموجبة الجزئية هنالك على الأقل فرد واحد تجتمع فيه «أ» و«ب» معًا؛ وفي حالة السالبة الجزئية هنالك على الأقل فرد واحد لا تجتمع فيه صفتا «أ» و«ب» معًا.
والآن فلنراجع ما ورد في المنطق التقليدي عما بين هذه «القضايا» الأربع من تقابل، وسنرى أنه — باستثناء ما جاء فيه عن تناقض القضايا — قد أخطأ في كل أحكامه.
- (١)
فالقضيتان «كل أ هي ب»، «بعض أ ليس ب» متقابلتان لأن موضوعهما هو «أ» ومحمولهما هو «ب» لكنهما مختلفتان في الكم؛ إذ إن أولاهما كلية والثانية جزئية، ومختلفتان كذلك في الكيف، لأن أولاهما موجبة والثانية السالبة، ويسمى هذا التقابل تناقضًا.
وعلاقة التناقض قائمة كذلك بين القضيتين «لا أ هي ب» و«بعض أ هي ب».
- (٢)
والقضيتان «كل أ هي ب» و«بعض أ هي ب» متقابلتان لأنهما متفقتان في الموضوع «أ» وفي المحمول «ب» لكنهما مختلفتان في الكم، فالأولى كلية والثانية جزئية، ويسمى هذا التقابل تداخلًا.
وعلاقة التداخل قائمة كذلك بين القضيتين «لا أ هي ب» و«بعض أ ليس ب».
- (٣)
والقضيتان الكليتان «كل أ هي ب» و«لا أ هي ب» متقابلتان لأنهما مشتركتان في الموضوع «أ» وفي المحمول «ب» لكنهما مختلفتان في الكيف، فالأولى موجبة والثانية سالبة، ويسمى هذا التقابل تضادًّا.
- (٤)
والقضيتان الجزئيتان «بعض أ هي ب» و«بعض أ ليس ب» متقابلتان لأنهما مشتركتان في الموضوع «أ» وفي المحمول «ب» لكنهما مختلفتان أيضًا في الكيف، فالأولى موجبة والثانية سالبة، ويسمى هذا التقابل دخولًا تحت التضاد.
وقد جرى العرف في كتب المنطق على تصوير هذه العلاقات الأربع بين «القضايا» الأربع، بمربع على النحو الآتي:
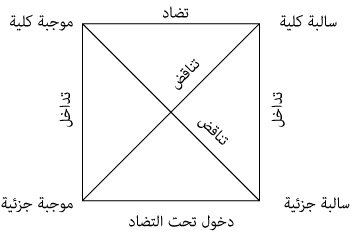
- (١)
فالتناقض يكون بين الكلية والجزئية المختلفين في الكيف.
- (٢)
والتداخل يكون بين الكلية والجزئية المتفقتين في الكيف.
- (٣)
والتضاد يكون بين الكليتين المختلفتين في الكيف.
- (٤)
والدخول تحت التضاد يكون بين الجزئيتين المختلفتين في الكيف.
- (١)
ففي حالة التناقض يكون إثباتنا لصدق قضية ما مساويًا لإنكارنا لصدق نقيضتها، والعكس صحيح؛ أي إن إنكارنا لصدق قضية ما مساوٍ لإثباتنا لصدق نقيضتها.
فإذا أثبتنا صدق الموجبة الكلية، كان ذلك بمثابة إنكارنا لصدق السالبة الجزئية، وإذا أثبتنا صدق السالبة الكلية، كان ذلك بمثابة إنكارنا لصدق الموجبة الجزئية؛ والعكس صحيح في كلتا الحالتين.
- (٢) وفي حالة التداخل يكون إثباتنا لصدق القضية الكلية ملزمًا بإثبات صدق القضية الجزئية الداخلة فيها، فلو قلنا إن «كل أ هي ب» صادقة، كانت «بعض أ هي ب» صادقة أيضًا؛ ولو قلنا «لا أ هي ب» صادقة كانت «بعض أ ليس ب» صادقة أيضًا.١
وكذلك إنكارنا لصدق القضية الجزئي ملزم بإنكار صدق القضية الكلية التي تحتويها، فلو قلنا إن «بعض أ هي ب» كاذبة كانت «كل أ هي ب» كاذبة أيضًا؛ ولو قلنا إن «بعض أ ليس ب» كاذبة، كانت «لا أ هي ب» كاذبة أيضًا.
والعكس في الحالتين غير صحيح، أي أننا لو أنكرنا صدق القضية الكلية فلا يجوز لنا أن ننكر تبعًا لذلك صدق القضية الجزئية الداخلة فيها، وكذلك لو أثبتنا صدق القضية الجزئية فلا يجوز أن نثبت تبعًا لذلك صدق القضية الكلية التي تحتويها.
- (٣)
وفي حالة التضاد يكون إثباتنا لصدق أحد الضدين مساويًا لإنكارنا صدق الضد الآخر، فلو كانت «كل أ هي ب» صادقة؛ كانت «لا أ هي ب» كاذبة ولو كانت «لا أ هي ب» صادقة كانت «كل أ هي ب» كاذبة.
لكن العكس غير صحيح، أي إننا لو أنكرنا صدق أحد الضدين فلا يجوز أن نثبت أو أن ننكر — تبعًا لذلك — صدق الضد الآخر.
- (٤)
وفي حالة الدخول تحت التضاد يكون إنكارنا لصدق إحدى القضيتين الداخلتين تحت التضاد مساويًا لإثباتنا صدق القضية الأخرى؛ فلو كانت «بعض أ هي ب» كاذبة كانت «بعض أ ليس ب» صادقة، ولو كانت «بعض أ ليس ب» كاذبة، كانت «بعض أ هي ب» صادقة.
ولكن العكس غير صحيح، أي إننا لو أثبتنا صدق إحدى القضيتين الداخلتين تحت التضاد، فلا يجوز لنا أن نثبت أو أن ننكر — تبعًا لذلك — صدق القضية الأخرى:
هذا ما يقوله المنطق التقليدي عن التقابل بين (القضايا) الأربع وما يستلزمه من أحكام عليها بالصدق أو الكذب.
- (١)
ففي حالة التداخل لا يجوز نستدل من صدق (القضية) الكلية صدق القضية الجزئية، فمن إثباتنا لصدق العبارة. «كل أ هي ب» لا يجوز أن نثبت الصدق أيضًا للعبارة: «بعض أ هي ب»؛ وكذلك من إثباتنا لصدق العبارة: «لا أ هي ب» لا يجوز أن نثبت الصدق أيضًا للعبارة «بعض أ ليس ب» لا يجوز ذلك إلا إذا كانت «أ» فئة ذات أفراد.
أما إذا كانت «أ» فئة فارغة بغير أفراد جزئية، فاستدلال صدق الجزئية من صدق الكلية غير جائز، ذلك لأن العبارة الكلية لا تشترط وجود أفراد بل هي عبارة شرطية معناها: إذا كان هناك فرد من أفراد «أ» فهذا الفرد هو «ب»، أما العبارة الجزئية فمعناها وجودي، لأن معناها هو. هنالك على الأقل فرد واحد «أ» بحيث يتصف هذا الفرد الواحد بأنه كذلك فرد في فئة «ب».
فالصدق في العبارة الكلية هو إثبات لعلاقة الشرط: إذا كان هنالك «أ» لزم عن ذلك أن تكون «ب»، وإذا أثبتنا الصدق لهذه العلاقة بين «أ» و«ب» فلا يبرر لنا ذلك أن نستدل أن أحد أفراد «أ» موجود فعلًا فمن عدم الوجود لا يجوز أن نستدل الوجود.
الصدق في العبارة الكلية لا يشترط فيه وجود أفراد الفئة التي نتحدث عنها، فلك أن تقول «كل عنقاء تجيد عدة لغات» وتزعم لها الصدق، ويكون المعنى المراد عندئذٍ هو: إذا وجدت فردًا من أفراد العنقاء؛ وجدتها تجيد عدة لغات.
أما الصدق في العبارة الجزئية فيقتضي وجود فرد واحد على الأقل من أفراد الفئة التي نتحدث عنها؛ فلو قلت «بعض العنقاوات يجيد عدة لغات أجنبية» وزعمت لهذا القول صدقًا، كان معنى الصدق هنا: أن فردًا واحدًا على الأقل من فئة العنقاوات موجود فعلًا، وهو يجيد عدة لغات. وما دام هذا هو ما تزعم، فعليك الإشارة إلى هذا الفرد الذي يحقق ما تزعمه.
وهكذا ترى أن «أ» إذا كانت فئة فارغة فإن قولي «كل أ هي ب» تكون صادقة، لكن لا يلزم عن ذلك صدق «بعض أ هي ب».
بل إن «أ» إذا كانت فئة فارغة، فكل عبارة كلية فيها «أ» يستوي فيها الصدق والكذب، فعبارة «كل أ هي ب» تكون صادقة أو كاذبة على السواء، وعبارة «لا أ هي ب» تكون صادقة أو كاذبة على السواء.
ليس في العالم (أنهار من عسل)، وإذًا فهذه فئة فارغة، وعلى ذلك فقولك (كل أنهار العسل تفيض في الشتاء) قول يستوي فيه الصدق والكذب، وكذلك قولك (أنهار العسل لا تفيض في الشتاء) يستوي فيه الصدق والكذب، وإذًا فلا يجوز من مثل هذا القول أن نستدل ما يأتي: (هنالك على الأقل نهر واحد من أنهار العسل يفيض في الشتاء) أو (هنالك على الأقل نهر واحد من أنهار العسل لا يفيض في الشتاء) لأن هاتين العبارتين الأخيرتين دالتان على وجود نهر من هذا القبيل وجودًا فعليًّا، وهو يوصف في العبارة الأولى بأنه يفيض في الشتاء، وفي الحالة الثانية بأنه لا يفيض في الشتاء وعلى القائل في هاتين الحالتين أن يدلنا على هذا النهر الجزئي الذي يتحدث عنه، وعلى ذلك فنحن الآن إزاء حالة لا يستوي فيها الصدق والكذب، لأن العالم الخارجي تتغير صورته بين حالتي الصدق والكذب.
ونعود بك إلى طريقة المنطق الرمزي في التعبير، لنوضح لك هذا في صورة جلية:٢إذا كانت أ = صفر
∴ أ × ب = صفر × ب = صفر … (١)وكذلك أ × ~ ب = صفر × ~ ب = صفر … (٢)أي إنه إذا كانت «أ» رمزًا لفئة فارغة، فإنك (١) إذا أضفت إلى أفراد هذه الفئة الفارغة صفة جديدة هي «ب» كان الناتج صفرًا أي فئة فارغة أيضًا، و(٢) إذا أضفت إلى أفراد هذه الفئة الفارغة صفة جديدة هي «لا − ب» كان الناتج صفرًا كذلك أي فئة فارغة.
ومعنى ذلك أن وصفك للفئة الفارغة بأنها «س» أو «لا − س» لا يغير من الأمر شيئًا.
لكن إذا كانت أ = صفر
فإن قولك أ ب ≠ صفرلا يكون قولًا صادقًا؛ إذ ما دامت «أ» تساوي صفرًا، فحاصل ضربها مع أي فئة أخرى لا بد أن يساوي صفرًا كذلك.
وكذلك إذا كانت أ = صفر
فقولك أ ~ ب ≠ صفرلا يكون قولًا صادقًا لنفس السبب، إذ ما دامت «أ» تساوي صفرًا، فحاصل ضربها مع «~ ب» لا بد أن يساوي صفرًاما معنى ذلك كله؟ معناه أنه إذا كانت «أ» فئة فارغة جاز لك أن تقول عنها إنها «ب» أو «لا − ب»، لكنه لا يجوز لك أن تثبت وجود فرد من أفراد «أ» ثم تصفه بأنه «ب» أو بأنه «لا − ب».
أي إنه من العبارة الكلية — موجبة كانت أو سالبة — لا يجوز لنا أن نستدل شيئًا عن العبارة الجزئية الداخلة فيها؛ وإذن فقد أخطأ المنطق التقليدي في تحليله لعلاقة التداخل وما تقتضيه من أحكام.
- (٢) وأخطأ المنطق التقليدي أيضًا في تحليله لعلاقة التضاد، لأنه زعم أننا من صدق أحد الضدين نستطيع أن نستدل كذب الضد الآخر، أي إننا من صدق العبارة: «كل أ هي ب» نستدل كذب العبارة: «لا أ هي ب»؛ وهذا زعم لا يصدق إلا إذا كانت «أ» فئة ذات أفراد، أما إذا كانت «أ» فئة فارغة فالضدان سواء من حيث الصدق والكذب، لأنه:
إذا كانت أ = صفر
∴ أ ب = صفر … وهذه هي السالبة الكليةوكذلك أ ~ = ب = صفر … وهذه هي الموجبة الكليةأي إنه إذا كانت «أ» فئة فارغة، فالعبارة الكلية التي ترد فيها «أ» تكون أيضًا مساوية لصفر، سواء كانت موجبة أو سالبة.
- (٣)
وكذلك قل في العلاقة بين القضيتين الجزئيتين الداخلتين تحت التضاد «بعض أ هي ب» و«بعض أ ليس ب» فلو كانت «أ» فئة فارغة، استحال علينا أن نقول أية عبارة من العبارتين، لأن كلتيهما تثبت وجود فرد على الأقل من أفراد «أ»، ثم تحكم عليه العبارة الأولى بأنه «ب»، والعبارة الثانية بأنه «ليس ب» وإذن فالقولان كاذبان معًا إذا كانت «أ» فئة فارغة ليس فيها هذا الفرد الواحد الذي تحكمان عليه.



