نظرية القياس
(١) تعريف القياس
ونقول إن هذا التطبيق للاستدلال القياسي، أضيق من التعريف الذي عرفه به أرسطو، لأن التعريف الذي أسلفناه قد ينطبق على عمليات استدلالية لا تكون حدودها ثلاثة فقط، ولا تكون الرابطة التي تربط تلك الحدود هي رابطة الموضوع والمحمول.
فالقياس — كما يفهم من التطبيق لا من التعريف — عملية استدلالية تتألف من ثلاث قضايا حملية فقط، ويحتوي على ثلاثة حدود فقط.
(٢) حدود القياس
من هذه الحدود الثلاثة التي يشتمل عليها القياس، حدان يظهران في النتيجة كما يظهران في المقدمتين، (كل منهما يظهر في مقدمة واحدة) وأما الحد الثالث فيظهر في المقدمتين ويختفي في النتيجة.
والحدان اللذان تتألف منهما النتيجة، يكون أحدهما موضوعًا ويكون الآخر محمولًا، فما يكون منهما محمولًا في النتيجة يسمى بالحد الأكبر، وما يكون منهما موضوعًا في النتيجة يسمى بالحد الأصغر؛ ويسمى هذان الحدان — الأكبر والأصغر معًا — بطرفي القياس.
وأما الحد الذي يظهر في كلتا المقدمتين معًا، ولا يظهر في النتيجة، فيسمى بالحد الأوسط؛ وهو الحد الذي يرتبط به الحدان الأكبر والأصغر معًا، فيلزم عن ذلك بالضرورة أن يكون بين هذين الحدين علاقة ما، نشأت عن اشتراكهما معًا في الحد الأوسط، وبذلك يلزم ارتباطهما معًا في النتيجة.
ونوضح ذلك بالصورة القياسية الآتية:
كل و − ك
كل ص − و
«ك» التي هي محمول النتيجة، هي الحد الأكبر.
«ص» التي هي موضوع النتيجة، هي الحد الأصغر
«و» التي تظهر في المقدمتين معًا وتختفي في النتيجة، هي الحد الأوسط وإنما سميت هذه الحدود بأسمائها تلك؛ لأنها — في مذهب أرسطو — تصف اتساع مجالها بنسبة بعضها إلى بعض؛ فالحد الأكبر يشير إلى فئة من الماصدقات أكبر فعلًا من الفئتين اللتين يشير إليهما الحدان الأوسط والأصغر؛ والحد الأوسط يشير إلى فئة تقع من حيث الاتساع بين فئة الحد الأكبر وفئة الحد الأصغر، والحد الأصغر يشير إلى أصغر الفئات فعلًا.
والشكل الآتي يصور هذه العلاقة الكمية بين الحدود الثلاثة:
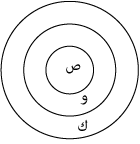
ولما كانت هذه العلاقة الكمية بين الحدود الثلاثة، لا تتمثل في وضوح إلا في القياس الذي أسلفنا صورته، أي القياس الذي تكون قضاياه الثلاثة موجبة كلية، ويكون الحد الأوسط فيه موضوعًا في القضية الأولى ومحمولًا في القضية الثانية، عدَّت هذه الصورة القياسية نموذجًا للقياس كله.
على أن هذه العلاقة بين الحدود، من حيث انطباق أسمائها (الأكبر، الأوسط، الأصغر) على اتساع مجال مسمياتها، لا تصدق في بعض الحالات الأخرى مما يعيب هذه التسمية، ولا يجعلها بذات مدلول صحيح.
فهي لا تصدق إذا كانت إحدى المقدمتين سالبة، وكذلك لا تصدق إذا كانت إحدى المقدمتين جزئية، عندئذٍ لا يكون هنالك حتم بأن يكون الحد الأكبر أكبر فعلًا في نطاق مسمياته، ولا الأصغر أصغر فعلًا، ولا الأوسط وسط فعلًا.
فالقياس الذي صورته:
لا و − ك
كل ص − و
يمكن أن تجيء صورته على النحو الذي يبينه الشكل الآتي:

وفيه ترى أن الحد الأكبر هو أصغر الحدود الثلاثة مجالًا، والأوسط أكبرها مجالًا.
والقياس الذي صورته:
لا و − ك
بعض ص − و
يمكن أن تجيء صورته على النحو الذي يبينه الشكل الآتي:

حيث ترى أن الأكبر أصغرها مجالًا، والأصغر أكبرها مجالًا.
(٣) قضايا القياس
يحتوي القياس (الحملي على قضايا ثلاث: مقدمتان ونتيجة وتسمى؛ إحدى المقدمتين بالكبرى لاشتمالها على الحد الأكبر، وتسمى الأخرى بالمقدمة الصغرى لاشتمالها على الحد الأصغر.
ففي القياس الذي صورته:
كل و − ك
كل ص − و
تكون الأولى هي المقدمة الكبرى، والثانية هي المقدمة الصغرى، والثالثة هي النتيجة.
إن الذي حدا بالمنطق التقليدي أن يجعل في القياس مقدمة كبرى، وأخرى صغرى، هو أن الاستدلال القياسي — وهو عندهم النموذج الوحيد الاستدلال الصحيح — بمثابة تطبيق قاعدة عامة على حقيقة أقل تعميمًا منها، ومشمولة فيها، وبهذا نحكم على الحقيقة الأصغر بما حكمنا به على الحقيقة الأكبر.
| أ على يمين ب، ب على يمين ﺟ | ∴ أ على يمين ﺟ |
| أ شمال ب، ب غربي ﺟ | ∴ أ على شمال غربي ﺟ |
| أ تساوي ب، ب تساوي ﺟ | ∴ أ تساوي ﺟ |
| أ أكبر من ب، ب أكبر من ﺟ | ∴ أ أكبر من ﺟ |
| أ قبل ب، ب قبل ﺟ | ∴ أ قبل ﺟ |
فها هنا نحن لا نسير في حركتنا الفكرية في خطوات مجزأة، كل منها تتألف من مقدمتين ونتيجة، على النحو الآتي:
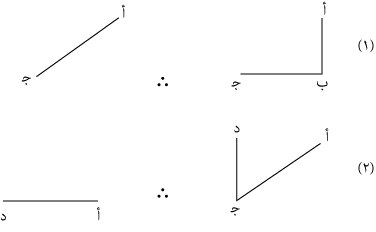
أقول إننا لا نجزئ حركة الفكر هذه التجزئة حتى نجعل كل خطوة استدلالًا قياسيًّا ذا حدود ثلاثة وقضايا ثلاث، بل نقيم البناء كله في الذهن أولًا دفعة واحدة، ثم نرى أين تقع د بالنسبة ﻟ أ؛ على النحو الآتي:

ويتضح من ذلك أننا — مهما كان عدد الخطوات — نظل نركب بعضها إلى بعض، ولا نصل إلى النتيجة إلا في النهاية، ولا تحديد هناك لعدد الخطوات المؤدية إلى النتيجة إلا قدرة الإنسان على الاستيعاب، فلو زادت الخطوات على قدرة الإنسان على استيعابها دفعة واحدة، اضطر إلى الوقوف في وسط الطريق ليخلص ما فات في نتيجة واحدة، ثم يواصل السير. لكنه لو استطاع استيعاب الخطوات كلها دفعة واحدة، فلا اضطرار هناك للوقوف والتجزئة، وإذن فضرورة تحديد الخطوات التي تكفي للاستدلال متوقفة على عوامل نفسية، لا على ضرورة منطقية.
(٤) قواعد القياس
- (١)
كل قياس يشتمل على ثلاثة حدود فقط.
- (٢)
كل قياس يشتمل على ثلاث قضايا فقط.
وأول ما يلاحظ على هاتين «القاعدتين» أنهما ليستا من قبيل القواعد التي تضمن سلامة الاستدلال؛ فهما «تعريف» للقياس، أو وصف له، وقد لا يستوفي الاستدلال هذين الشرطين، ومع ذلك يكون استدلالًا سليمًا من الوجهة الصورية مثال؛ ذلك:
ب أكبر من ﺟ
أ أكبر من ب
∴ أ أكبر من ﺟفها هنا استدلال سليم، يتألف من قضايا ثلاث، لكنه يشتمل على أكثر من ثلاثة حدود هي: (١) ب، (٢) أكبر من ﺟ، (٣) أ، (٤) أكبر من ب.
فيقول أنصار القياس ردًّا على ذلك، إن مثل هذا الاستدلال لا يكون قياسًا، فنحن نشترط للاستدلال كي يكون قياسًا — هكذا قد يقول هؤلاء الأنصار — أن يكون مشتملًا على ثلاثة حدود فقط وثلاثة قضايا فقط، وما لا يتوافر فيه هذان الشرطان لا يكون قياسًا؛ بل يكون استدلالًا من نوع آخر، أطلقوا عليه ما شئتم من أسماء.
لكن مثل هذا الرد في رأي «برادلي»، حجة على أنصار القياس لا حجة لهم، لأن نقطة الخلاف ليست هي: بماذا نسمي هذه العملية الاستدلالية وأشباهها؟ بل نقطة الخلاف الرئيسية هي: هل الاستدلال القياسي هو الصورة الوحيدة للاستدلال الصحيح أو هناك صورة أخرى سواه؟ فإن سلمتم بأن هناك صورًا أخرى غير القياس، يكون فيها الاستدلال سلمًا، انهار أساس من أسس المنطق الأرسطي الذي لم يعترف إلا بالقياس وحده «نموذجًا» للتفكير السليم، فإما أن يجيء التفكير على صورة قياسية مباشرة، وإلا فلا بد — في رأي ذلك المنطق — أن يكون من الممكن رده إلى صورة قياسية حتى نطمئن إلى أنه تفكير سليم.
- (٣)
يجب أن يكون الحد الأوسط مستغرقًا في إحدى المقدمتين على الأقل هذه قاعدة سليمة، تتبين ضرورتها من الرسوم الآتية التي نوضح بها مقدمتين لم يستغرق الحد الأوسط في إحداهما، ولذا ترى أن العلاقة بينهما يمكن تصويرها على احتمالات خمسة، وما دام الأمر كذلك فلا ضمان هناك بالصورة الصحيحة منها؛ وبالتالي لا ضمان هناك يؤكد النتيجة التي تنتزع منهما.
والمقدمتان اللتان نصورهما بالرسوم الآتية هما: «كل ك − و» و«كل ص − و» [الحد الأوسط «و» ليس مستغرقًا لأنه محمول قضية موجبة كلية في الحالتين].
 شكل ١٣-٤فمن هذه الاحتمالات الخمسة للعلاقة بين المقدمتين المذكورتين يمكن استنتاج واحدة من نتائج خمس، هي:
شكل ١٣-٤فمن هذه الاحتمالات الخمسة للعلاقة بين المقدمتين المذكورتين يمكن استنتاج واحدة من نتائج خمس، هي:- (١)
كل ص هي كل ك.
- (٢)
كل ص − ك.
- (٣)
كل ك − ص.
- (٤)
بعض ص − ك، أو بعض ك − ص.
- (٥)
لا ص − ك أو لا ك − ص.
ومعنى هذا التعدد في النتائج استحالة الوصول إلى نتيجة محدودة من المقدمتين فإذا استنتجنا نتيجة من مقدمتين ليس الحد الأوسط مستغرقًا في إحداهما، نشأت عن ذلك المغالطة المعروفة باسم «مغالطة الوسط غير المستغرق».١٤ - (١)
- (٤)
لا يجوز استغراق حد في النتيجة ما لم يكن مستغرقًا في إحدى المقدمتين:
وهذه أيضًا قاعدة سليمة، لأننا نستمد النتيجة من المقدمتين، فما لم تكن المقدمتان قد حكمتا على فئة معينة بكل أفرادها، فلا يجوز بداهة أن نستنتج حكمًا على هذه الفئة بكل أفرادها، ما دمنا لا نريد الخروج على حدود ما جاء في المقدمتين.
فإذا كان الحد الأكبر (أي محمول النتيجة) هو الذي استغرق في النتيجة ولم يكن مستغرقًا في إحدى المقدمتين، نشأت عن ذلك المغالطة المعروفة باسم «مغالطة التجاوز في الحد الأكبر»؛١٥ وإذا كان الحد الأصغر (أي موضوع النتيجة) هو الذي استغرق في النتيجة ولم يكن مستغرقًا في إحدى المقدمتين، نشأت عن ذلك المغالطة المعروفة باسم «مغالطة التجاوز في الحد الأصغر».١٦ - (٥)
لا إنتاج من مقدمتين سالبتين.
والرسوم الخمسة الآتية تبين احتمالات خمسة للعلاقة بين «ص» و«ك» — وهما حدا النتيجة — إذا كانت المقدمتان هما: «لا و − ك» و«لا ص − و».
 شكل ١٣-٥فمن هذه الاحتمالات الخمسة لصورة العلاقة بين «ص» و«ك» يمكن استنتاج واحدة من النتائج الخمس الآتية:
شكل ١٣-٥فمن هذه الاحتمالات الخمسة لصورة العلاقة بين «ص» و«ك» يمكن استنتاج واحدة من النتائج الخمس الآتية:- (١)
كل ص هي كل ك.
- (٢)
كل ص − ك.
- (٣)
كل ك − ص.
- (٤)
بعض ص − ك، أو بعض ك − ص.
- (٥)
لا ص − ك، لا ك − ص.
ومعنى هذا أن التعدد في النتائج الممكن استدلالها من المقدمتين، استحالة الوصول إلى نتيجة محددة.
لكن من علماء المنطق فريقًا لا يأخذ بهذه القاعدة في القياس، ويرى أن المقدمتين السالبتين قد تنتجان، فهذا «جفنز»١٧ يسوق لنا المثل الآتي لقياس منتج مقدمتاه سالبتان: كل ما ليس بمعدني لا تكون له القدرة على التأثير المغناطيسي القوي؛ والكربون ليس معدنيًّا، وإذن فالكربون ليس قادرًا على التأثير المغناطيسي القوي.فها هنا مقدمتان سالبتان، ومع ذلك نراهما تنتجان نتيجة سالبة صحيحة.
ويرد «كينز»١٨ على هذا النقد قائلًا إن هذا الاستثناء الظاهري للقاعدة ليس بالاستثناء الحقيقي لها، نعم إنه لا شك في صحة الاستدلال في هذا المثل الذي أورده «جفنز»، ويمكن الرمز له بما يأتي:لا «لا − و» − «ك»
ولا «ص» − «و»
∴ لا «ص» − «ك»لكننا إذا اعتبرنا المقدمتين سالبتين، كان لدينا أربعة حدود، هي (١) لا − و، (٢) ك، (٣) ص، (٤) و، وعلى ذلك لا يكون الاستدلال قياسيًّا لأنه جاوز شرط القياس الذي يحتم ألا تزيد الحدود عن ثلاثة.
ولكي نحول هذا الاستدلال إلى الصورة القياسية، وجب أن نحول المقدمة الصغرى (بواسطة عملية نقض المحمول) إلى موجبة كلية بحيث تصبح: كل «ص، − ولا − و» وعندئذٍ يكون الاستدلال كما يأتي:
لا «لا − و» «ك»
كل «ص» «لا − و»
∴ لا «ص» «ك»وهو استدلال قياسي بالمعنى الصحيح، لم نجاوز فيه شرط الحدود الثلاثة، وإلا فلو تساهلنا في شرط الحدود الثلاثة، كان من الممكن أن نحول كل قياس سليم إلى قياس ذي مقدمتين سالبتين (بواسطة نقض المحمول) فمثلًا هذا القياس الآتي:
كل «و» − «ك»
كل «ص» − «و»
∴ كل «ص» − «ك»يصبح بواسطة نقض المحمول في المقدمتين كما يأتي:
لا «و» «لا − ك»
لا «ص» «لا − و»
∴ لا «ص» «لا − ك»فهل نقول في مثل هذه الحالة إننا قد استطعنا الاستنتاج من مقدمتين سالبتين؟ كلا، لأن الحدود ليست ثلاثة في هذه الصورة، وإذن فليست هي بالصورة القياسية.
وهذا دفاع طيب عن «كينز» عن القياس» كما تحدد معناه عند أرسطو؛ لكنه يتضمن أيضًا أن الاستدلال قد يكون صحيحًا دون أن يكون استدلالًا قياسيًّا، وإذن، فليس الاستدلال القياسي بشروطه وقواعده هو النموذج الوحيد للتفكير السليم، كما ظن الأرسطيون؛ وفي ذلك يقول «برادلي»١٩ دفاعًا عن وجهة نظر «جفنز» إنه على الرغم من أن القياس الذي ذكره يحتوي على أربعة حدود، وأنه بذلك يخالف الصورة الفنية للقياس، إلا أن ذلك لا ينفي أننا قد وصلنا إلى نتيجة من مقدمتين سالبتين، هما: (١) «أ ليست ب» و(٢) «ما ليس ب لا يكون ﺟ» «إذن أ ليست ﺟ» ثم يمضي برادلي في حديثه فيقول: «وإذا استطعت من مقدمتين سالبتين أن أصل إلى نتيجة، فلا غناء لي في الاعتراض بأني قد وصلت إلى ذلك بتحويل إحدى المقدمتين من صورة إلى صورة، لأن ذلك الاعتراض لا يدل على أن المقدمتين ليستا سالبتين، ولا يدل على أني قد أخفقت في الوصول إلى نتيجة».٢٠والخلاصة التي نريد نحن أن ننتهي بقارئنا إليها، هي أن المقدمتين السالبتين لا تنتجان ما دمنا نحافظ على شرط الحدود الثلاثة في القياس، لكن تجاوز هذا الشرط ممكن، وعندئذٍ يجوز أن نصل إلى نتائج سليمة من مقدمات سالبة، وإذا لم نشأ أن تسمى هذه الصورة الجديدة باسم «القياس» فسمها بما شئت لها من أسماء، لكنها صورة صالحة للاستدلال الصحيح، وإذن فليس القياس بمعناه المعروف هو الوسيلة الوحيدة للاستدلال.
- (١)
- (٦)
إذا كانت إحدى المقدمتين سالبة، وجب أن تكون النتيجة سالبة، والعكس صحيح، أي إننا إذا أردنا إقامة البرهان على نتيجة سالبة، فلا بد أن تكون إحدى المقدمتين سالبة.
وهذه القاعدة — مع ثانية النتائج التي سنذكرها فورًا — إن هما إلا تطبيق لمبدأ بديهي، وهو أن النتيجة تتبع أضعف المقدمتين في الكم والكيف على السواء؛ ولما كان السلب يعتبر أضعف من الإيجاب، لزم أن تكون النتيجة سالبة إذا كانت إحدى المقدمتين سالبة، كذلك لما كانت الجزئية أضعف من الكلية لزم أن تكون النتيجة جزئية إذا كانت إحدى المقدمتين جزئية.
(٥) نتائج تلزم عن قواعد القياس
-
(١)
لا إنتاج من مقدمتين جزئيتين.
لأن المقدمتين الجزئيتين إما أن تكونا:
-
(أ)
جزئيتين سالبتين، أو
-
(ب)
جزئيتين موجبتين، أو
-
(جـ)
جزئية موجبة ومعها جزئية سالبة.
والحالة الأولى لا تنتج بناءً على القاعدة الخامسة.
والحالة الثانية لا تنتج بناءً على القاعدة الثالثة التي تشترط وجوب استغراق الحد الأوسط في إحدى المقدمتين على الأقل، إذا ما دامت المقدمتان جزئيتين موجبتين، فلن يكون فيهما أي حد مستغرقًا؛ وبالتالي لا يتوافر شرط استغراق الحد الأوسط.
وأما الحالة الثالثة فلا تنتج بناءً على القاعدتين الثالثة والرابعة، وهما قاعدتا الاستغراق في القياس. وذلك لأننا إذا استنتجنا نتيجة من مقدمتين إحداهما جزئية موجبة والأخرى جزئية سالبة، لزم أن تكون النتيجة سالبة بناءً على القاعدة السادسة؛ لكن النتيجة السالبة لا بد أن يكون محمولها مستغرقًا، وإذن فلا بد أن يكون هذا المحمول مستغرقًا أيضًا في المقدمة التي ورد فيها؛ وعلى ذلك يتحتم أن يكون في المقدمتين حدان مستغرقان على الأقل. أحدهما الحد الأوسط وثانيهما يكون هو هذا المحمول في النتيجة؛ ولما كان المقدمة الموجبة الجزئية لا تستغرق حدًّا من حديها، والمقدمة السالبة الجزئية تستغرق حدًّا واحدًا فقط، كانت المقدمتان لا تشتملان إلا على حد مستغرق واحد، فإن كان هو الحد الذي سنجعله محمولًا للنتيجة لزم أن يكون الحد الأوسط غير مستغرق في المقدمتين وهو ما لا يجوز، وإن كان هو الحد الأوسط، لزم أن يكون الحد الذي هو محمول مستغرق في النتيجة السالبة، غير مستغرق في المقدمة التي ورد فيها، وهو ما لا يجوز كذلك وإذن فلا إنتاج من مثل هاتين المقدمتين.
-
(أ)
-
(٢)
إذا كانت إحدى المقدمتين جزئية، وجب أن تكون النتيجة جزئية لأن الحالة عندئذٍ لا بد أن تكون واحدة من الفروض الثلاثة الآتية:
-
(أ)
المقدمتان سالبتان، وإحداهما جزئية.
-
(ب)
المقدمتان موجبتان، وإحداهما جزئية.
-
(جـ)
مقدمة موجبة وأخرى سالبة، وإحداهما جزئية.
فالحالة الأولى لا تنتج بناءً على القاعدة الخامسة.
والحالة الثانية إذا أنتجت، وجب أن تكون الجزئية جزئية موجبة، لأن المقدمتين (الموجبة الكلية والموجبة الجزئية) لا تستغرقان فيما بينهما إلا حدًّا واحدًا فقط (هو موضوع الموجبة الكلية) ولا بد من جعل هذا الحد الواحد المستغرق حدًّا أوسط ليتحقق شرط استغراق الحد الأوسط في إحدى المقدمتين على الأقل؛ وعلى ذلك فلا يتبقى حد مستغرق في المقدمتين، يجيز لنا أن ننقله إلى النتيجة مستغرقًا، فلا مندوحة لنا عن أن تكون النتيجة خالية من الاستغراق في حديها معًا، وذلك لا يتوافر إلا إذا كانت النتيجة موجبة جزئية.
وفي الحالة الثالثة لا يمكن المقدمتين معًا أن تشتملا على أكثر من حَدَّيْن مستغرقين، أحدهما لا بد أن يكون هو الحد الأوسط، وإذن فلا يتبقى للنتيجة إلا حد مستغرق واحد؛ لكن النتيجة لا بد أن تكون سالبة، ما دامت إحدى المقدمتين سالبة، فلا مندوحة عن أن نجعلها سالبة جزئية لنتطلب حدًّا مستغرقًا واحدًا هو محمولها.
-
(أ)
-
(٣)
لا إنتاج من مقدمة كبرى جزئية ومقدمة صغرى سالبة.
لأنه ما دامت المقدمة الصغرى سالبة فلا بد أن تكون المقدمة الكبرى موجبة (بحكم القاعدة الخامسة التي توجب عدم الاستقلال القياسي من مقدمتين سالبتين)، لكن هذه المقدمة الكبرى الموجبة هي جزئية كذلك (بحكم الفرض)، وإذن فالحد الأكبر في النتيجة، وهو ما أخذناه لها من المقدمة الكبرى، ليس مستغرقًا في المقدمة، ويجب أن يظل غير مستغرق في النتيجة كذلك (بناءً على القاعدة الرابعة) أي لا بد أن تكون النتيجة موجبة، لكنها يجب كذلك أن تكون سالبة لأن إحدى المقدمتين سالبة (بناءً على القاعدة السادسة) وعلى ذلك فالإنتاج من هاتين المقدمتين مستحيل.
(٦) استنتاج بعض قواعد القياس من بعضها الآخر
- (أ)
قاعدتا الكم (الاستغراق).
(١) لا بد من استغراق الحد الأوسط في مقدمة واحدة على الأقل.
(٢) لا يجوز استغراق حد في النتيجة ما لم يكن مستغرقًا في المقدمة التي ورد فيها.
- (ب)
قاعدتا الكيف.
(٣) لا إنتاج من مقدمتين سالبتين.
(٤) إذا كانت إحدى المقدمتين سالبة، وجب أن تكون النتيجة سالبة، وللبرهنة على نتيجة سالبة وجب أن تكون إحدى المقدمتين سالبة.
ويمكن وضع قاعدتي الكيف على هذه الصورة، للبرهنة على نتيجة موجبة، لا بد أن تكون المقدمتان موجبتين معًا؛ وللبرهنة على نتيجة سالبة، لا بد أن تكون إحدى المقدمتين موجبة والأخرى سالبة.
- (١)
فالقاعدة القائلة إن المقدمتين السالبتين لا تنتجان، يمكن استنتاجها من القاعدة القائلة إن الحد الأوسط يجب أن يستغرق في إحدى المقدمتين على الأقل.
وفيما يلي طريقة للبرهان على ذلك:٢١خذ أي مقدمتين سالبتين، وضع الحدين في كل منهما أي وضع تشاء، فسيمكنك بواسطة عملية العكس أن تغير من مواضع حدودهما حتى يصبحا على الصورة الآتية:
لا ك − و
لا ص − و
ثم انقض المحمول في كل منهما، تحصل عليهما في الصورة الآتية:
كل «ك» «لا − و»
كل «ص» «لا − و»
وها هنا نرى حدًّا أوسط، هو «لا − و» غير مستغرق في إحدى المقدمتين ومن ثم يتبين أن القاعدة الثالثة نتيجة تلزم عن القاعدة الأولى.
- (٢)
قاعدتا السلب يمكن استنتاج إحداهما من الأخرى.
فيمكن استنتاج قاعدة أنه إذا كانت إحدى المقدمتين سالبة وجب أن تكون النتيجة سالبة، من قاعدة ألا إنتاج من مقدمتين سالبتين، وذلك على النحو الآتي:
إذا فرضنا أن مقدمتين «ق» و«ك» تبرهنان على نتيجة «م» فإن «ق» بالإضافة إلى نفي «م» تبرهنان على نفي «ك» وذلك لأن «ق» و«ك» لا تكونان صادقتين معًا إلا إذا صدقت معها النتيجة، «م»، فإذا نقضنا «م» كان لا بد من نقض إحدى المقدمتين «ق» أو «ك».
نضع ذلك وضعًا آخر فنقول:
إذا كان لدينا قياس هذه صورته:
ق
ك
∴ مفإنه ينتج عن ذلك ما يأتي:
ق
م
∴ ككما ينتج أيضًا ما يأتي:
ك
م∴ قفإذا فرضنا جدلًا أن المقدمة السالبة ق والمقدمة الموجبة ك تنتجان معًا نتيجة موجبة م، فإنه بناءً على الطريقة السابقة لو نقضنا م وجعلناها مقدمة مع ق نتجت لنا نقيض ك هكذا:قمكلكن هذه الصورة لا تجوز بحكم الفرض الذي سلمنا به، وهو أن المقدمتين السالبتين لا تنتجان، وإذن فالفرض الذي فرضناه جدلًا لا يمكن صدقه وهو أن تنتج نتيجة موجبة من مقدمتين إحداهما سالبة.
بهذا أقمنا البرهان على أنه من قاعدة ألا إنتاج من مقدمتين سالبتين يمكن استنتاج قاعدة الكيف الأخرى.
وبنفس الطريقة يمكن أن نقيم البرهان على أنه من القاعدة القائلة بأنه لو كانت إحدى المقدمتين سالبة فإن النتيجة تكون سالبة، يمكن استنتاج قاعدة الكيف الأخرى التي تقضي بألا إنتاج من سالبتين، هكذا:
افرض جدلًا أنه يمكن أن نستنتج قضية سالبة من مقدمتين سالبتين هكذا:
قك∴ ملو صح ذلك، لصح كذلك ما يأتي:
قم
∴ كلكن هذه الصورة الثانية تخالف ما فرضنا التسليم بصحته أولًا، وهو وجوب أن تكون النتيجة سالبة لو كانت إحدى المقدمتين سالبة، إذن فهذه الصورة الثانية غير جائزة؛ وبالتالي لا تجوز الصورة الأولى التي أنتجتها، أعني أنه لا يجوز أن نستدل نتيجة من مقدمتين سالبتين معًا.
- (٣)
قاعدة الكم يمكن استنتاج إحداهما من الأخرى.
من القاعدة القائلة بأن الحد الأوسط لا بد من استغراقه في إحدى المقدمتين على الأقل يمكن استنتاج القاعدة الثانية وهي أنه لا يجوز أن نستغرق حدًّا في النتيجة ما لم يكن مستغرقًا في المقدمة التي ورد فيها.
وطريقة البرهان كما يلي:
افترض جدلًا أن لدينا القياس الآتي:و − ك
ص − و
∴ ص − كوافرض كذلك جدلًا أن «ك» مستغرقة في النتيجة ولم تكن مستغرقة في المقدمة الكبرى.
ثم انقض النتيجة وضعها مقدمة صغرى هكذا:
و − ك
(ص − ك)∴ (ص − و)وعندئذٍ ترى أن القياس الذي نشأ لك، قياس حده الأوسط هو «ك» وهو حد غير مستغرق في إحدى المقدمتين؛ فهو غير مستغرق في المقدمة الكبرى بحكم الفرض، وهو غير مستغرق المقدمة الصغرى، لأنها نقيض لقضية كانت «ك» فيها غير مستغرقة؛ والقاعدة هي أن الحد المستغرق في قضية ما يصبح غير مستغرق في نقيضها) وعلى ذلك تكون هذه الصورة القياسية الأخيرة فاسدة بحكم قاعدة الاستغراق الأولى التي فرضنا صدقها؛ وبالتالي تكون صورة القياس المعادلة لها، والتي فرضنا صدقها جدلًا، فاسدة كذلك؛ ومعنى ذلك أننا لو خرجنا على قاعدة الاستغراق الثانية، انتهينا إلى قياس فاسد بحكم قاعدة الاستغراق الأولى، مما يدل على أن القاعدة الثانية يمكن استنتاجها من القاعدة الأولى.ويمكن اتباع نفس الطريقة للبرهنة على أن قاعدة الاستغراق الأولى، يمكن استنتاجها من القاعدة الثانية.
وذلك بأن نفرض جدلًا فرضًا تخرج فيه على القاعدة الأولى، تجد أنك قد انتهيت إلى حالة لا تصح بحكم القاعدة الثانية، وهكذا:افرض جدلًا صحة القياس الآتي:
كل ك − و
كل ص − و
∴ كل ص − كها هنا الحد الأوسط «و» غير مستغرق في إحدى المقدمتين؛ ولو كان هذا القياس صحيحًا، لترتب عليه صحة ما يأتي:
كل ك − و
بعض ص ليس ك. (نقيض النتيجة في القياس الأصلي)
بعض ص ليس و. (نقيض الصغرى في القياس الأصلي)
لكن محمول النتيجة هنا، وهو «و» مستغرق في النتيجة، وليس مستغرق في المقدمة الكبرى، إذن فهو قياس فاسد بحكم القاعدة التي فرضنا صحتها، وهي أنه لا يجوز استغراق حد في النتيجة ما لم يكن مستغرقًا في المقدمة التي ورد فيها؛ وعلى ذلك يكون القياس الذي يعادله فاسدًا أيضًا، وهو القياس الذي فرضنا جدلًا أنه صحيح، والذي خرجنا فيه عمدًا على حكم قاعدة الاستغراق الأولى لنرى ماذا تكون نتيجة هذا الخروج بالنسبة لقاعدة الاستغراق الثانية.
عد الآن إلى قاعدتي الكم (١)، (٢) وقاعدتي الكيف (٣)، (٤)، تر مما أسلفناه، أن الجزء الأول من القاعدة الرابعة يلزم عن القاعدة الثالثة، وإذن فيمكننا الاستغناء عنه؛ وأن القاعدة الثالثة بدورها يلزم عن القاعدة الأولى، وإذن فيمكننا الاستغناء عنها؛ وأن القاعدة الأولى والثانية تلزم كل منهما عن الأخرى حتى لنستطيع أن نجعل إحداهما نتيجة للأخرى، وإذن فيمكن الاستغناء عن إحداهما حسب اختيارنا.
وعلى هذا لا يبقى لدينا إلا القاعدة الأولى وحدها (أن إن شئنا فالقاعدة الثانية وحدها) مضافًا إليها الجزء الثاني من القاعدة الرابعة.
وبهذا تكون قاعدتا القياس الأساسيتان هما:
-
(١)
قاعدة الكم.
لك أن تختار فيها إما قاعدة الاستغراق الأولى، أو قاعدة الاستغراق الثانية وتستغني بالتي تختارها من الأخرى.
-
(٢)
قاعدة الكيف.
وهنا يمكن الأكفاء بالجزء الثاني وحده من جزئي القاعدة الرابعة، وهو: «للبرهنة على نتيجة سالبة يجب أن تكون إحدى المقدمتين سالبة».
ويلاحظ أن القياس الوحيد الذي يكون فاسدًا على أساس هذه القاعدة الثانية، دون أن يكون فاسدًا على أساس قاعدة الكم، هو هذا:
كل ك − و
كل و− ص
بعض ص ليس ك
وهو قياس من الشكل الرابع (انظر أشكال القياس في الفصل الآتي) وإذن فكل قياس سليم في الأشكال الثلاثة الأولى، يكفي فيه توافر قاعدة واحدة هي قاعدة الكم التي تختارها قاعدتي الاستغراق.
على أن تلخيص قواعد القياس كلها في قاعدة واحدة على هذا النحو، لا ينجينا من ضرورة مراجعة كل قياس على القواعد الأربع، لأنه قد يحدث أن تجد قياسًا متفقًا مع قاعدة الكم اتفاقًا ظاهرًا، حتى إذا ما حللنا الموقف وجدنا أن فيه فسادًا بطريق غير مباشر.
فافرض — مثلًا — أنك قد جعلت قاعدتك الوحيدة في الكم هي وجوب استغراق الحد الأوسط في إحدى المقدمتين، فإن قياسًا كهذا:
كل و − ك
لا ص − و
لا يتضمن خروجًا مباشرًا على القاعدة، ولكن حلل الموقف، يتبين لك أنه لو كان هذا القياس صحيحًا لصح ما يأتي:
كل و − ك
بعض ص − ك (نقيض النتيجة في القياس الأصلي)
لكننا نرى أن الحد الأوسط في هذا القياس (وهو «ك») غير مستغرق في إحدى المقدمتين؛ وعلى ذلك فإن قاعدتنا نفسها التي أخذناها، تقتضي فساد القياس الأصلي، لكن فساده لا يظهر إلا بطريق غير مباشر.
(٧) مبدأ الاستدلال القياسي
هذه القواعد التي أسلفنا ذكرها وتحليلها، إنما هي نتائج تترتب على مبدأ الاستدلال القياسي عند أرسطو؛ أعني أنها أصبحت قواعد، لأن أرسطو تصور الاستدلال القياسي على صورة معينة، ولا تتحقق هذه الصورة إلا إذا روعيت تلك القواعد، فهو يجعل مبدأ الاستدلال القياسي كله متمثلًا في القياس الذي يكون فيه الحد الأوسط موضوعًا في المقدمة الكبرى ومحمولًا في المقدمة الصغرى (وهو ما يسمى قياسًا من الشكل الأول كما سيأتي في الفصل التالي).
وسنشرح معنى هذا على الصورة القياسية الآتية:
كل و − ك
كل ص − و
كل ص − ك
هنا قد حملنا «ك» على «و» في المقدمة الكبرى، أي حملناها على حد مستغرق، لأن «و» في تلك المقدمة مستغرقة؛ وما دمنا قد حملنا «ك» على «و» فقد أصبح جائزًا لنا أن نحمل «ك» هذه على أي شيء يندرج تحت «و»، ولما كانت المقدمة الصغرى تبين أن «ص» مندرجة تحت «و» فيمكن حمل «ك» عليها في النتيجة، بحيث نقول: «كل ص − ك».
-
(١)
يبيح المبدأ أن يكون في القياس ثلاثة حدود فقط، وهي: (أولًا) حد لا بد أن يكون مستغرقًا؛ (ثانيًا) حد نحمله على ذلك الحد المستغرق (ثالثًا) حد يندرج تحت ذلك الحد المستغرق، وهذه الحدود هي على التوالي: الحد الأوسط والحد الأكبر والحد الأصغر.
-
(٢)
ويبيح المبدأ أن يكون القياس مشتملًا على ثلاث قضايا فقط؛ وهي (أولًا) قضية تحمل حدًّا ما على حد مستغرق، (ثانيًا) وقضية أخرى تنص على أن حد ما مندرج تحت ذلك الحد المستغرق، (ثالثًا) وقضية تصف ذلك الحد المندرج تحت الحد المستغرق بما وصف به الحد المستغرق نفسه، وهذه القضايا هي على التوالي: المقدمة الكبرى، والمقدمة الصغرى، والنتيجة.
-
(٣)
يشترط المبدأ أن يكون الحد الأوسط مستغرقًا في مقدمة واحدة على الأقل، بل يشترط كذلك أن تكون هذه المقدمة هي الكبرى.
-
(٤)
القاعدة القائلة بعدم استغراق الحد الأكبر في النتيجة ما لم يكن مستغرقًا في المقدمة الكبرى، متضمن في المبدأ بطريقة غير مباشرة، لأن هذه الغلطة في القياس لا تقع إلا إذا كانت النتيجة سالبة، لكن عبارة «بالطريقة نفسها» الواردة في المبدأ تنص على أنه إذا كان ثمة نتيجة سلبية، وجب أن تكون المقدمة الكبرى سلبية كذلك، ولما كان الحد الأكبر في أي قياس ينطبق عليه المبدأ انطباقًا مباشرًا هو محمول المقدمة الكبرى، فسيكون هذا الحد الأكبر في حالة سلب المقدمة الكبرى مستغرقًا في مقدمته كما هو مستغرق في النتيجة.
وعدم استغراق الحد الأصغر في النتيجة ما لم يكن مستغرقًا في المقدمة الصغرى، مشروط عليه في المبدأ، إذ إن المبدأ لا يبيح لنا أن نحمل في النتيجة إلا على موضوع قد تبين فعلًا في المقدمة الصغرى أنه مندرج تحت الحد الأوسط.
-
(٥)
القضية التي تنص على أن شيئًا ما مندرج تحت الحد الأوسط المستغرق لا بد بالضرورة أن تكون قضية موجبة، وعلى ذلك فالمبدأ يشترط ألا تكون المقدمتان سالبتين معًا.
-
(٦)
عبارة «بالطريقة نفسها» الواردة في المبدأ، تضمن صراحة المحافظة على سلامة القاعدة القائلة بأنه إذا كانت إحدى المقدمتين سالبة وجب أن تكون النتيجة سالبة، والعكس صحيح أيضًا، لأنه إذا كان المحمول في المقدمة الكبرى منفيًّا عن الموضوع، فسنجعل هذا المحمول نفسه منفيًّا كذلك عن الموضوع في النتيجة.
نقد هذا المبدأ:
قد تقول ولكني حين أعمم في المقدمة الأولى، لا أريد الناس فردًا فردًا، لأن إحصاءهم على هذا النحو مستحيل، إنما أريد النوع بصفة عامة، لكن إذا كان أمرك كذلك، فكيف استطعت أن تخصص الحكم على محمد؛ إن محمدًا ليس هو النوع بصفة عامة، إنما هو فرد متعين متخصص، فحكمك عليه بما حكمت به على النوع بصفة عامة، هو في حقيقة الأمر قياس باطل لأنه يحتوي على أربعة حدود:
(الإنسان فان) إنسان في الحالة الأولى معناها «النوع بصفة عامة»
(محمد إنسان) إنسان في الحالة الثانية معناها متعين في شخص معروف
هكذا ترى مبدأ القياس — بالصورة النموذجية الساقة — معيبًا في ذاته، وحتى لو لم يكن معيبًا، لما كان من السعة بحيث يشمل كل أنواع الاستدلال الصحيح ويسوق «برادلي» طائفة من أمثلة استدلالية ليست تندرج تحت الصورة النموذجية للقياس، أسلفنا بعضها، ونعيد ذكره هنا لزيادة الإيضاح:
لكن «برادلي» يتهم هذا المبدأ بالسعة كما اتهم المبدأ الأول بالضيق، لأننا سنجد أمثلة ينطبق عليها هذا المبدأ، ومع ذلك فهي أمثلة لاستدلال باطل، مثل قولنا «أ أسرع جريًا من ب وب عنده كلب (ﺟ)»؛ «أ أثقل وزنًا من ب وب أسبق من (ﺟ)»؛ «أ أغلى ثمنًا من ب، ب على المنضدة (ﺟ)»، «أ تشبه ب، ب تشبه ﺟ» — في هذه الأمثلة يصعب الوصل بين أ − ﺟ.
قد يقال هنا دفاعًا عن المبدأ، إن هذه الأمثلة مغالطات، فإذا كان لا يمكن الاستدلال من «أ تشبه ب، ب تشبه ﺟ» فلأن النقطة التي تشبه ب فيها أ، غير النقطة من ب التي تشبه فيها ﺟ؛ وإذا لم يكن الاستدلال من «أ أغلى ثمنًا من ب، ب على المنضدة (ﺟ)» فلأن الجانب من ب الذي يجعلها أرخص ثمنًا من أ، غير الجانب الذي يجعلها على المنضدة؛ وهكذا قل في سائر الأمثلة، وإذن فنحن في هذه الأمثلة لا نستعمل «ب» أي الحد المشترك، بمعنى واحد، فنكون بمثابة من يستعمل حدين، وعلى ذلك لا تكون أ، ﺟ مرتبطتين بشيء واحد بعينه كما ينص المبدأ».
لكنه على سبيل التوضيح يذكر أربعة مبادئ أو خمسة:
-
(١)
مبدأ التآلف بين الموضوع والمحمول:
(أ) صفات الموضوع الواحد مرتبط بعضها ببعض.
(ب) إذا تشابه موضوعان في صفة، أو اختلفا، فهما بالتالي يكونان متشابهين أو مختلفين.
أمثلة:
(أ) هذا الرجل منطقي، وهذا الرجل أحمق، إذن فالمنطق قد يكون أحمق (أي يكون أحمق بالفعل لو تحققت ظروف معينة).
(ب) هذا الكلب أبيض وهذا الحصان أبيض (أو بني) فهذا الكلب وهذا الحصان متشابهان (أو مختلفان).
-
(٢)
مبدأ تآلف الذاتية (الهوية):
إذا اشترك حد مع حدين أو أكثر في نقطة بعينها، كانت هذه الحدود الأخرى مشتركة في هذه النقطة ذاتها.
أمثلة:
قطعة النقد أ فيها نفس النقش الذي على قطعة النقد ب، وقطعة ب فيها نفس النقش الذي على ﺟ، وإذن أ، ﺟ متشابهان في النقش.
إذا كان أ شقيق ب، ب شقيق ﺟ، ﺟ أخت د، إذن أ شقيق د.
-
(٣)
مبدأ تآلف الدرجة:
إذا ارتبط حد — في جانب معين من جوانبه — برباط الدرجة مع حدين آخرين أو أكثر، كانت هذه الأخرى مرتبطة برباط الدرجة أيضًا.
أمثلة: أ أشد حرارة من ب، ب أشد حرارة من ﺟ، إذن أ أشد حرارة من ﺟ.
اللون أ أكثر بريقًا من ب، ب أكثر بريقًا من ﺟ، إذن أ أكثر بريقًا من ﺟ.
-
(٤)
(٥) مبدأ تآلف الزمان وتآلف المكان:
إذا ارتبط حد معين بحدين آخرين أو أكثر برابطة الزمان أو المكان، كان لا بد من وجود الرابطة الزمانية أو الرابطة المكانية بين هذه الحدود الأخرى. أمثلة. أ شمالي ب، ب غربي ﺟ ∴ ﺟ جنوبي شرقي أ.أ يوم سابق لحادثة ب؛ وحادثتا ب، ﺟ متعاصرتان، إذن أ يوم سابق لحادثة ﺟ.
بهذه المبادئ المختلفة للاستدلال، يحاول «برادلي» أن يبين أن مبدأ الاستدلال القياسي كما هو في دائرته الضيقة التي تجعل العلاقة بين الحدود علاقة موضوع ومحمول، مبدأ لا يصلح وحده أساسًا، ولا بد من تعديله من جهة، وإضافة مبادئ أخرى من جهة أخرى، حتى تشمل كل ضروب الاستدلال الصحيح.
وإذا صح رأي لوكاشفتش كان ما نعرضه هنا هو الصورة التقليدية للقياس الأرسطي، وليس هو القياس الأرسطي كما ورد في صورته الأصلية.
بصدد هذا المبدأ يقول لوكاشفتش (نظرية القياس الأرسطية: ترجمة الدكتور عبد الحميد صبرة، ص٦٨): «لست أرى كيف يمكن أن ينتج عن هذا المبدأ … الضرب من الشكل الثالث الذي مقدمته الكبرى موجبة كلية ومقدمته الصغرى موجبة جزئية ونتيجته موجبة جزئية … ولا بد من توكيد القول إن أرسطو ليس مسئولًا عن هذا المبدأ الغامض، ولا يصدق أن مبدأ «المقول على كل وعلى لا واحد» قد وضعه أرسطو مسلمة بنى عليها كل استدلال قياسي، كما ذهب إلى ذلك كينز …».



