أشكال القياس وضروبه

(١) أشكال القياس

سنستخدم فيما يلي الرموز الآتية بمعانيها الآتية:

ك = الحد الأكبر

و = الحد الأوسط

ص = الحد الأصغر

م = موجبة كلية

ب = موجبة جزئية

ل = سالبة كلية

س = سالبة جزئية

فإذا كتبنا صيغة كهذه: «و (م) ك» كان معناها «قضية موجبة كلية موضوعها الحد الأوسط ومحمولها الحد الأكبر».

وإذا كتبنا صيغة كهذه: «ص (ب) و» كان معناها «قضية موجبة جزئية موضوعها الحد الأصغر ومحمولها الأوسط» وهكذا.

وللقياس أشكال مختلفة تختلف باختلاف وضع الحد الأوسط في المقدمتين.

لكنك مع ذلك قد تستطيع أن تستنتج منهما أن بعض الشيوعيين ليسوا نساءً.

ك − و

و − ص

ص − ك

ويمضي «جوزف» في بحثه ليدل على أن الحدين الأكبر والأصغر لم يطلق عليهما اسماهما لمجرد كون الأول محمول النتيجة والثاني موضوعها، بل لأن الأكبر أكبر فعلًا والأصغر أصغر فعلًا في معظم الحالات، وخصوصًا في الحالات التي يكون فيها الاستدلال علميًّا، تعبر قضاياه عن معرفة بالمعنى الصحيح.

فليس في مستطاعنا دائمًا أن نعكس حدي النتيجة بحيث نجعل موضوعها محمولًا ومحمولها موضوعًا، دون أن نجاوز بذلك حدود الأوضاع الصحيحة للأمور؛ نعم إننا في قضية مثل «بعض العلماء ساسة» يمكن أن نعكس الحدين فنقول «بعض الساسة علماء» دون أن يكون هنالك شيء من شذوذ، لأن التقاء العلم والسياسة في شخص أو أشخاص التقاء عرضي، فلا بأس في أن أحمل السياسة على العلم أو العلم على السياسة، فالمعنيان سواء.

أما حين يكون الموضوع فردًا والمحمول صفة تميزه، فمن القسر أن أعكس الوضع بحيث أجعل الفرد محمولًا على الصفة، فقولي: قيصر قائد عظيم، قول يتفق مع الأوضاع الطبيعية، لأني أحمل فيه الصفة على موصوفها، أما إذا عكست الحدين فقلت: أحد القواد العظماء قيصر، فقلب لما ينبغي أن يكون.

فإذا استثنينا الحالات التي يكون التقاء الموضوع والمحمول فيها عرضًا، وجدنا أن المحمول عادة يكون أوسع مجالًا من موضوعه، لأنه شيء ينتمي إليه ذلك الموضوع هو وغيره من الموضوعات، وليس العكس صحيحًا، أي ليس المحمول جزءًا من مجال الموضوع؛ ومن الطبيعي أن يحمل الجنس على النوع، والصفة على الموصوف لا العكس، وبخاصة في القضايا العلمية التي تكون كلية، فلا بد — إن لم يتساوَ المحمول والموضوع في مجال الماصدق — أن يكون المحمول أوسع مجالًا، لأننا لا نستطيع أن نعمم الحكم في قضية كلية، إذا كان المحمول لا ينطبق إلا على بعض أفراد الموضوع فقط دون بعض.

فحين أطلق أرسطو على محمول النتيجة في القياس اسم الحد الأكبر، فقد اختار الاسم المطابق لواقع الحال، حين يكون الموضوع فردًا، وحين يكون الموضوع أقل شمولًا من المحمول، وعلى ذلك يكون المحمول شاملًا للموضوع المذكور في النتيجة ولغيره مما عساه أن يقع معه في نوع واحد تحت الجنس الذي نعبر عنه بالحد الأكبر، والذي هو المحمول.

ونخلص من هذا إلى أن «جالينوس» قد أخطأ حين جعل الشكل الرابع شكلًا قائمًا بذاته من أشكال القياس، يكون الحد الأوسع شمولًا من حدي النتيجة هو موضوعها، والحد الأضيق شمولًا منهما هو محمولها؛ وهو وضع — كما قلنا — لا يتفق مع طبائع الأمور.

ففي قياس كهذا:

ما يتناسل بسرعة قصير الأجل

والذباب يتناسب بسرعة

لو أردنا أن نجعله شكلًا رابعًا قائمًا بذاته، جعلنا محمول القضية الكبرى موضوعًا في النتيجة، وموضوع الصغرى محمولًا في النتيجة فتكون النتيجة هي: «بعض ما هو قصير الأجل ذباب».

وأما إذا أردنا أن نعتبره قياسًا من الشكل الأول، كانت النتيجة هي؛ «الذباب قصير الأجل».

ومن ذلك ترى كيف تكون النتيجة طبيعية في الشكل الأول، قسرية فيما يسمى بالشكل الرابع.

الصيغة الرمزية للحالة الأولى هي:

ك (ل) و

و (م) ص

والصيغة الرمزية للحالة الثانية هي:

ك (ل) و

و (ب) ص

وفي كلتا الحالتين لا يصلح الاستدلال من الشكل الأول [لأن الحد الأكبر سيكون مستغرقًا في النتيجة السالبة وليس مستغرقًا كمحمول للمقدمة الكبرى الموجبة الكلية في الحالة الأولى، والموجبة الجزئية في الحالة الثانية].

(٢) ضروب القياس

لئن كانت أشكال القياس تختلف باختلاف وضع الحد الأوسط، فاختلاف الضروب يتوقف على اختلاف الكم والكيف في القضايا التي يتألف منها القياس؛ وقد يتحد الكم والكيف في شكلين مختلفين من أشكال القياس، كما قد يختلف الكم والكيف في الشكل الواحد.

ترى الشكل واحدًا في الحالتين (وهو الشكل الأول) لكن الكم والكيف مختلفان في القضايا التي يتألف منها كل منهما، فهما في الحالة الأولى: موجبة كلية، وموجبة كلية، والنتيجة موجبة كلية؛ وفي الحالة الثانية: سالبة كلية، فموجبة كلية والنتيجة سالبة كلية.

قارن المثل (٢) بالقياس الآتي:

الفيلسوف المثالي لا يعترف بحقيقة الأشياء في الخارج … سالبة كلية

وكل العلماء الطبيعيين يعترفون بحقيقة الأشياء في الخارج … موجبة كلية

ترَ أن الكم والكيف في القضايا لا يتألف منها القياسان متشابهان، لأنهما في كلتا الحالتين: سالبة كلية فموجبة كلية، والنتيجة سالبة كلية، غير أن القياسين من شكلين مختلفين، القياس الأول من الشكل الأول والقياس الثاني من الشكل الثاني.

ننتقل الآن إلى البحث في أي الضروب في الأشكال المختلفة، يؤدي إلى نتائج صادقة، بعبارة أخرى: ما هي الصورة المختلفة التي تتركب على غرارها المقدمتان من حيث الكم والكيف، فتنتهيان إلى نتيجة صحيحة؟

الضروب الممكنة كلها — ما ينتج منها وما لا ينتج — ست عشرة هي: [لاحظ أننا كما أسلفنا. سنرمز بالرمز م للموجبة الكلية، وبالرمز ب للموجبة الجزئية، وبالرمز ل للسالبة الكلية، وبالرمز س للسالبة الجزئية].

فإذا طبقنا القواعد التي أسلفنا ذكرها في الفصل السابق، والتي لا بد من توافرها في أي قياس صحيح، يخرج من هذه الضروب الست عشرة ما يأتي:

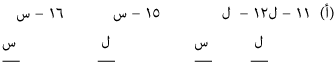
لأنها مؤلفة من مقدمتين سالبتين: وذلك لا يتفق مع القاعدة الخامسة من قواعد القياس.

لأنها مؤلفة من جزئيتين، وذلك لا يتفق مع أولى النتائج التي تترتب على قواعد القياس.

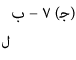
لأنها مؤلفة من كبرى جزئية وصغرى سالبة، وهو لا يتفق مع ثالثة النتائج المترتبة على قواعد القياس.

إذن فهذه ضروب ثمانية لا تنتج في أي شكل من أشكال القياس، لخروجها على القواعد الأساسية العامة، فيبقى لنا من الضروب ثمانية، هي:

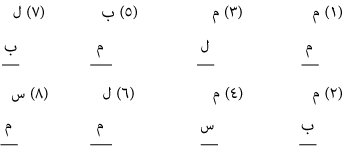
غير أن ما يصلح من هذه الضروب في شكل ما، قد لا يصلح في شكل آخر؛ أعني أنك قد تجد ضربًا من هذه الضروب الثمانية المنتجة، صالحًا في قياس من الشكل الأول — مثلًا — وغير صالح في شكل آخر.

من ذلك يمكن أن نستخلص القواعد الآتية لكل شكل على حدة:

(٣) التقتير في نتيجة القياس

وفيما يلي الحالات الخمس التي يمكن فيها أن نستنتج نتيجة جزئية مع إمكاننا استنتاج نتيجة كلية:

(أ) في الشكل الأول:

(١) و (م) ك

ص (م) و

(٢) و (ل) ك

ص (م) و

(ب) في الشكل الثاني:

(١) ك (ل) و

ص (م) و

(٢) ك (م) و

ص (ل) و

(ﺟ) في الشكل الرابع:

ك (م) و

و (ل) ص

ويلاحظ أن التقتير في النتيجة لا يكون في أي ضرب من ضروب الشكل الثالث، لأن جميع الضروب في هذا الشكل نتائجها جزئية، ولا يكون التقتير إلا حين يكون لدينا نتيجة كلية، و«نكتفي» في النتيجة بالجزئية الداخلة فيها.

على أن هذه «القناعة» بنتيجة أقل مما يجوز لنا أن نستنتجه ليس لها قيمة عملية — حتى لو فرضنا أنها جائزة منطقيًّا، إذ إنه من وجهة نظرنا لا يجوز أن نستنتج جزئية من كلية — نقول إن هذه «القناعة» بالنتيجة الجزئية في الوقت الذي يمكننا فيه أن نستنتج نتيجة كلية ليس لها قيمة عملية، ولا هي مما نتوقع حدوثه من أحد؛ إذ ما دام في مستطاع من يقيم البرهان على شيء أن يقيم برهانه على «الكل» فلماذا يكتفي بإقامة برهانه على «البعض»؟

ومن ثَم كانت الضروب المقترة كثيرًا ما تحذف من قوائم الضروب المنتجة.

(٤) الإفراط في مقدمات القياس

و (م) ك

و (م) ص

فالنتيجة في هذا القياس يمكن الحصول عليها من المقدمتين التاليتين:

و (م) م ك

و (ب) ص

أو من المقدمتين التاليتين:

و (ب) ك

و (م) ص

وكل قياس فيه مقدمتان كليتان ونتيجة جزئية، يكون قياسًا مفرطًا ما عدا هذا الضرب الآتي من ضروب الشكل الرابع:

ك (م) و

و (ل) ص

وذلك لأنه ما دامت إحدى المقدمتين سالبة، فستكون النتيجة سالبة كذلك، وسيكون محمولها مستغرقًا، وهذا المحمول هو نفسه موضوع المقدمة الكبرى الموجبة، إذن فلا بد أن تكون المقدمة الكبرى كلية حتى تضمن استغراق موضوعها، ولا يجوز لنا أن نضع مكانها الجزئية الموجبة، وإلا أصبح محمول النتيجة مستغرقًا مع عدم استغراقه في المقدمة الكبرى.

وكذلك في المقدمة الصغرى لا يجوز أن نضع السالبة الجزئية مكان السالبة الكلية، وإلا أصبح موضوعها غير مستغرق؛ مع أن موضوعها هو الحد الأوسط ولم يكن استغراق في المقدمة الكبرى، بحكم كونه هناك محمولًا لقضية موجبة، فلم يعد بد من استغراقه في المقدمة الصغرى؛ وبالتالي لم يعد بد من جعل المقدمة الصغرى سالبة كلية.

وعلى ذلك، فلا إفراط في مقدمات هذا الضرب من ضروب الشكل الرابع، على الرغم من أن المقدمتين كليتان والنتيجة جزئية.

وإذا استثنينا الضرب وحده، كانت لدينا القاعدة العامة التي ذكرناها، وهي أن كل قياس مقدمتاه كليتان ونتيجته جزئية، هو قياس مفرط، أي في إحدى مقدمتيه إفراط، لكونها كلية ويمكن الاكتفاء بالجزئية الداخلة فيها، لنصل إلى نفس النتيجة.

وفيما يلي ضروب القياس التي يكون فيها إفراط:

(أ) في الشكل الأول:

(١) و (م) ك

ص (م) و

(٢) و (ل) ك

ص (م) و

(ب) في الشكل الثاني:

(١) ك (ل) و

ص (م) و

(٢) ك (م) و

ص (ل) و

(ﺟ) في الشكل الثالث:

(١) و (م) ك

و (م) ص

(٢) و (ل) ك

و (م) ص

(د) في الشكل الرابع:

(١) ك (م) و

و (م) ص

(٢) ك (ل) و

و (م) ص

ويلاحظ أنه في حالتي الشكل الأول والثاني، يمكن اعتبار القياس الذي في إحدى مقدمتيه إفراط، قياسًا في نتيجته تقتير؛ والعكس صحيح، أي أن القياس الذي يكون في نتيجته تقتير، يمكن كذلك اعتباره قياسًا مفرطًا في إحدى مقدمتيه.

(٥) ملاحظة عامة على الأشكال الأربعة وضروبها المنتجة