زائر

  • ePub Logo
  • PDF Logo
  • Kindle Logo
الفصل السادس عشر

القياس الشرطي والقياس المركب

(١) القياس الشرطي المزدوج١

سنطلق هذا الاسم «القياس الشرطي المزدوج» على القياس إذا كانت كلتا المقدمتين شرطيتين.

مثل:

إذا صدقت ك صدقت م

وإذا صدقت ق صدقت ك

∴ إذا صدقت ق صدقت م

وإذا اعتبرنا المقدم في نتيجة القياس بمثابة الحد الأصغر، واعتبرنا التالي بمثابة الحد الأكبر، أمكن وضع القياس الشرطي المزدوج في الأشكال الأربعة التي عرفناها للقياس الحملي.

فالمثل السابق من الشكل الأول، لأن الحد الأوسط وهو «ك» موضوع في المقدمة الكبرى ومحمول في المقدمة الصغرى.

وفيما يلي مثل للقياس الشرطي المزدوج من الشكل الثاني، الذي يكون فيه الحد الأوسط محمولًا في المقدمتين:

يستحيل إذا صدقت م أن تصدق ك

وإذا صدقت ق صدقت ك

∴ يستحيل إذا صدقت ق أن تصدق م

هاك مثلًا آخر لقياس شرطي مزدوج من الشكل الثالث، الذي يكون فيه الحد الأوسط موضوعًا في المقدمتين:

إذا صدقت م صدقت ك

وإذا صدقت م صدقت ق

∴ قد يحدث أحيانًا أنه إذا صدقت ق صدقت ك

وهاك مثلًا أخيرًا لقياس شرطي مزدوج من الشكل الرابع، الذي يكون فيه الحد الأوسط محمولًا في المقدمة الكبرى، وموضوعًا في المقدمة الصغرى:

إذا صدقت ك صدقت م

ويستحيل إذا صدقت م أن تصدق ق

∴ يستحيل إذا صدقت ق أن تصدق ك

(٢) القياس الشرطي الحملي٢

سنطلق هذا الاسم «القياس الشرطي الحملي» على القياس إذا كانت مقدمته الكبرى شرطية، ومقدمته الصغرى حملية، وعندئذٍ تكون النتيجة حملية.

مثال ذلك:

إذا صدقت ق صدقت ك

لكن ق صادقة

∴ ك صادقة

ولهذا القياس ضربان:

  • (١)

    ضرب تجيء فيه القضية الحملية مثبتة للمقدم، وعندئذٍ تكون النتيجة إثباتًا للتالي، وقد يسمى هذا النوع بالبنائي، والمثل السابق يوضحه.

  • (٢)

    ضرب تجيء فيه القضية الحملية منكرة للتالي، وعندئذٍ تكون النتيجة تكذيبًا للمقدم، وقد يسمى هذا النوع بالهدمي.

مثال ذلك:

إذا صدقت ق صدقت ك

لكن ك كاذبة

∴ ق كاذبة

أما نفي المقدمة أو إثبات التالي، فلا يجوز أن ينتج نتيجة بالنسبة للشطر الثاني من شطري القضية الشرطية.

(٣) القياس المقتضب٣

القياس المقتضب هو الذي لم تذكر كل أجزائه؛ فتحذف منه إحدى مقدمتيه أو نتيجته، بحيث يكون الجزء المحذوف مفهومًا ضمنًا لا تصريحًا، وذلك هو ما يحدث في أغلب الأحيان حين يأخذ الحديث مجراه العادي المألوف من الحياة الجارية؛ ولذلك تراه كثيرًا ما يؤدي إلى المغالطة؛ إذ إن حذف مقدمة أو نتيجة يجعل الخطأ أخفى على السامع مما ذكر القياس بصورته الكاملة.

  • (أ)

    فإذا اقتضبت المقدمة الكبرى من قياس، سمى قياسًا مقتضبًا من الدرجة الأولى، مثل: معلقة امرئ القيس من الشعر الجاهلي، ولذلك ترى فيها ذكر الطلول.

    ولو أكملنا هذا القياس، قلنا: كل قصائد الشعر الجاهلي فيها ذكر للطلول ومعلقة امرئ القيس من الشعر الجاهلي، إذن فهي تذكر الطلول.

  • (ب)

    وإذا اقتضبت المقدمة الصغرى من قياس، سمي قياسًا مقتضبًا من الدرجة الثانية، مثل: كل قصائد الشعر الجاهلي فيها ذكر للطلول، ولذلك ترى معلقة امرئ القيس فيها ذلك.

  • (جـ)

    وإذا اقتضيت النتيجة من قياس، سمي قياسًا مقتضبًا من الدرجة الثالثة، مثل كل قصائد الشعر الجاهلي فيها ذكر للطلول، ومعلقة امرئ القيس من الشعر الجاهلي.

(٤) القياس المركب٤

هو ما يتألف من عدة أقيسة؛ بحيث تكون نتيجة القياس السابق مقدمة في القياس الذي يليه.

ويسمى القياس الذي تكون نتيجته مقدمة للذي يليه، قياسًا سابقًا،٥ كما يسمى القياس الذي تكون إحدى مقدمتيه نتيجة للذي سبقه، قياسًا لاحقًا.٦

ويمكن للقياس الواحد في هذه السلسلة أن يكون سابقًا ولاحقًا في آن واحد سابقًا بالنسبة لما يليه، ولاحقًا بالنسبة لما سبقه.

مثال للقياس المركب:

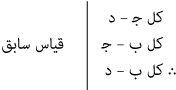
  • (أ)
    ويكون القياس المركب «متقدمًا»٧ حين يكون السير من قياس سابق إلى قياس لاحق، كما ترى في المثال السابق، فها هنا نقدم المقدمات أولًا، ونظل سائرين قدمًا في خطوات متتابعة من الاستدلال، حتى نصل إلى النتيجة الختامية التي تترتب على السلسلة كلها:

    وقد يسمى هذا النوع أيضًا باسم القياس المركب التركيبي.

  • (ب)
    ثم يكون القياس المركب «راجعًا»٨ حين يكون السير من قياس لاحق إلى قياس سابق، مثل:

    كل أ − د

    لأن كل أ − ب

    وكل ب − د

    لأن كل ب − ﺟ

    وكل ﺟ − د

    فها هنا نبدأ بالنتيجة النهائية ثم نقفل راجعين في خطوات متتابعة من البرهان حتى نصل إلى المقدمات التي بنيت عليها تلك النتيجة.

    وقد يسمى هذا النوع باسم القياس المركب التحليلي.

  • (جـ)

    وربما يحدث أحيانًا أن تقتضب الأقيسة التي يتألف منها قياس مركب وعندئذٍ نسميه بالقياس المركب المقتضب، مثال ذلك:

    كل ب − ﺟ لأنها د

    وكل أ − ب

    ∴ كل أ − ﺟ

    فها هنا ترى المقدمة الكبرى نتيجة لقياس اقتضبنا إحدى مقدمتيه ولو كتبناه كاملًا، قلنا:

    كل د − ﺟ

    كل ب − د

    ∴ كل ب − ﺟ

(٥) القياس المفصول النتائج٩

هو قياس مركب حذفت كل نتائجه ما عدا النتيجة النهائية، وجاءت مقدماته بحيث تشمل كل مقدمتين متتابعتين منها حدًّا مشتركًا، وينقسم قسمين:

(٥-١) القياس المفصول النتائج الأرسطي١٠

وفيه تكون المقدمة الأولى محتوية على موضوع النتيجة، ويكون الحد المشترك في أي مقدمتين متتابعتين محمولًا في أولاهما وموضوعًا في الثانية.

وهاك مثلًا له:

كل أ − ب

وكل ب − ﺟ

وكل − د

وكل د − ﻫ

∴ كل أ − ﻫ
فلو رددنا الأجزاء المقتضبة في هذه السلسلة، لكان لنا بذلك ثلاثة أقيسة هي:١١
  • (١)

    كل ب − ﺟ

    كل أ − ب

    ∴ كل أ − ﺟ
  • (٢)

    كل ﺟ − د

    كل أ − ﺟ

    ∴ كل أ − د
  • (٣)

    كل د − ﻫ

    كل أ − د

    ∴ كل أ − ﻫ
وفيما يلي مثل يوضح هذا النوع من القياس المفصول النتائج، مأخوذ من «ليبنتز»١٢ وهو يقيم البرهان على خلود الروح الإنسانية، غير أنه في سلسلة حجاجه كثيرًا ما نراه قد انحرف عن مجرى أقيسته المتتابعة ليؤيد قضية هنا أو قضية هناك؛ وفيما يلي سنضع القضايا التي لا تدخل في سلسلة القياس خارج السلسلة، لكي تتضح للقارئ الأقيسة المتتابعة في مجرى التفكير:
  • (١)

    الروح الإنسانية شيء فاعليته التفكير.

  • (٢)

    والشيء الذي فاعليته التفكير، تدرك فاعليته إدراكًا مباشرًا كأنه كل بغير أجزاء.

  • (٣)

    والشيء الذي يدرك على هذا النحو، لا تكون لفاعليته أجزاء.

  • (٤)

    والشيء الذي ليس لفاعليته أجزاء، هو شيء فاعليته ليست من قبيل الحركة … لأن كل حركة يمكن تقسيمها إلى أجزاء.

  • (٥)

    والشيء الذي ليست فاعليته حركة لا يكون جسمًا … لأن فاعلية الجسم حركة دائمًا.

  • (٦)

    وما ليس جسمًا لا يكون في مكان … لأن تعريف الجسم هو ما له امتداد.

  • (٧)

    وما ليس في مكان لا يكون قابلًا للحركة.

  • (٨)

    وما لا يقبل الحركة لا يمكن أن يتحلل. لأن التحلل هو حركة الأجزاء.

  • (٩)

    وما هو مستحيل التحلل مستحيل الفساد … لأن الفساد معناه تحلل الأجزاء الداخلية.

  • (١٠)

    وما ليس يفسد يكون خالدًا.

    ∴ فالروح الإنسانية خالدة.

(٥-٢) القياس المفصول النتائج الجو كليني١٣

وفيه تكون المقدمة الأولى محتوية على محمول النتيجة، ويكون الحد المشترك في أي مقدمتين متتابعتين؛ موضوعًا في أولاهما ومحمولًا في الثانية. مثال ذلك:

كل د − ﻫ

كل ﺟ − د

كل ب − ﺟ

كل أ − ب

∴ كل أ − ﻫ

ولو رددنا الأجزاء المقتضبة في هذه السلسلة، لكان لنا بذلك ثلاثة أقيسة، هي:

(١) كل د − ﻫ

كل ﺟ − د

∴ كل ﺟ − ﻫ

(٢) كل ﺟ − ﻫ

كل ب − ﺟ

∴ كل ب − ﻫ

(٣) كل ب − ﻫ

كل أ − ب

∴ كل أ − ﻫ

ويلاحظ أنه في القياس المفصول النتائج الأرسطي، تكون المقدمة الأولى والنتائج المقتضبة، هي المقدمات الصغرى في الأقيسة المتتابعة.

على حين أنه في القياس المفصول النتائج الجو كليني، تكون المقدمة الأولى والنتائج المقتضبة هي المقدمات الكبرى في الأقيسة المتتابعة.

(٦) قاعدتا القياس المفصول النتائج الأرسطي

  • (١)

    لا يجوز أن تزيد المقدمات السالبة على واحدة، فإن كانت هنالك مقدمة سالبة، وجب أن تكون هي الأخيرة.

  • (٢)

    لا يجوز أن تزيد المقدمات الجزئية على واحدة، فإن كانت هنالك مقدمة جزئية، وجب أن تكون هي الأولى.

أما أن المقدمات السالبة لا ينبغي أن تزيد على واحدة، لأننا لو استعملنا مقدمتين سالبتين، فسنجد عند تحليلنا للقياس المركب إلى أقيسة مستقلة، أن قياسًا منها ذو مقدمتين سالبتين؛ ثم ما دامت إحدى المقدمات سالبة، فالنتيجة ستكون سالبة، بالتالي سيكون محمولها مستغرقًا، وإذن فلا بد أن يكون مستغرقًا كذلك في المقدمة التي وَرَدَ فيها، أي في المقدمة الأخيرة، لذلك وجب أن تكون هذه الأخيرة هي السالبة لو كان هنالك مقدمة واحدة سالبة.

وعلى ذلك فلا بد لجميع المقدمات. ما عدا الأخيرة أن تكون موجبة، وإذا كانت إحدى هذه المقدمات الموجبة جزئية، وجب أن تكون هي الأولى، وإلا وجدنا أنفسنا إزاء قياس مستغرق في حده الأوسط.

(٧) قاعدتا القياس المفصول النتائج الجو كليني

هما قاعدتا القياس الأرسطي، مع تبادل كلمتي «الأولى» و«الأخيرة» ووضع كل منهما مكان الأخرى، فهما:

  • (١)

    لا يجوز أن تزيد المقدمات السالبة على واحدة، فإن كانت هنالك مقدمة سالبة، وجب أن تكون هي الأولى:

  • (٢)

    لا يجوز أن تزيد المقدمات الجزئية على واحدة فإن كانت هنالك مقدمة جزئية، وجب أن تكون هي الأخيرة.

(٨) قياس الإحراج

هو نوع من القياس يتركب من مقدمتين:

  • (أ)

    الأولى تشمل قضيتين شرطيتين (أو أكثر) معطوفتين.

  • (ب)

    والثانية تشمل إثباتًا للمقدمين في المقدمة الأولى، أو إنكارًا للتاليين فيها.

مثل ذلك:

إذا صدقت ق صدقت ك، وإذا صدقت ل صدقت م.

لكنه إما أن تصدق ق أو تصدق ل

∴ فلا بد إما أن تكون ك صادقة أو تكون م صادقة.
وأهم ما يميز قياس الإحراج هو أن الاختيار يتحتم بين بديلين كلاهما مكروه، ومن ثم يصفون الشخص الذي يقع عليه الإحراج بأنه «متورط على قرني الإحراج».١٤

والإحراج يبنى إذا كانت مقدمته الصغرى تثبت المقدمين في المقدمة الكبرى، ويهدم إذا كانت مقدمته الصغرى تنفي التاليين في المقدمة الكبرى.

ويكون الإحراج البنائي «بسيطًا» إذا كان التاليان في المقدمة الكبرى غير مختلفين، ويكون «مركبًا» إذا كان التاليان في المقدمة الكبرى مختلفين وكذلك يكون الإحراج الهدمي «بسيطًا» إذا كان المقدمان في الكبرى غير مختلفين، ويكون «مركبًا» إذا المقدمان في الكبرى مختلفين.

وعلى ذلك يكون لقياس الإحراج صور أربع، هي:

(٨-١) الإحراج البنائي البسيط

وصورته هي:

إذا صدقت ق صدقت ك، وإذا صدقت ل صدقت ك

ولكن إما أن تصدق ق أو تصدق ل

∴ فلا بد أن تكون ك صادقة

مثال ذلك أن يقال للجنود المحصورين بين العدو القوي من جهة والبحر من جهة أخرى:

إذا قاومتم هلكتم (بسيف العدو) وإذا تقهقرتم هلكتم (غرقًا)

لكنكم إما أن تقاوموا أو أن تتقهقروا

إذن فلا بد في كلتا الحالتين أن تهلكوا

(٨-٢) الإحراج البنائي المركب

وصورته هي:

إذا صدقت ق صدقت ك، وإذا صدقت ل صدقت م

لكنه إما أن تصدق ق أو تصدق ل

∴ فلا بد أن تصدق ك أو أن تصدق م

مثال ذلك:

إذا أكثرت من التحصيل العلمي، زاد مقدار ما تنساه من حقائق؛ وإذا لم تكثر من التحصيل العلمي، فلن تتسع معارفك.

لكنك إما أن تكثر من التحصيل العلمي أو لا تكثر منه، إذن فلا بد لك من إحدى الحالتين، فإما أن يزيد مقدار ما تنساه من حقائق، أو لا تتسع معارفك.

(٨-٣) الإحراج الهدمي البسيط

وصورته هي:

إذا صدقت ق صدقت ك، وإذا صدقت ق صدقت ل

إما أن تكون ك كاذبة أو تكون ل كاذبة

∴ فلا بد أن تكون ق كاذبة

مثال ذلك (المثل مأخوذ من جمهورية أفلاطون، الجزء الثالث، فقرة ٣٩١)

إن كان هومر صادقًا فيما رواه عن الآلهة، كان الأبطال أبناء الآلهة، وكان هؤلاء الأبطال أيضًا رجالًا أشرارًا.

لكنه إما ألا يكون الأبطال أبناء الآلهة، وإما أن يكونوا رجالًا أشرارًا، وإذن يكون هومر كاذبًا — في كلتا الحالتين — فيما رواه.

(٨-٤) الإحراج الهدمي المركب

وصورته هي:

إذا صدقت ق صدقت ك، وإذا صدقت ل صدقت م

لكنه إما أن تكون ك كاذبة، أو تكون م كاذبة

∴ فلا بد إما أن تكون ق كاذبة أو أن تكون ل كاذبة

مثال ذلك (من قول كاتب إنجليزي).

إذا أعطينا المستعمرات حكمًا ذاتيًّا، جعلناها قوية، وإذا أبقينا عليها سلطاننا جعلناها أعداءنا.

لكنه ينبغي إما ألا نجعلها قوية أو ألا نجعلها أعداءنا.

وإذن فينبغي إما ألا نعطيها حكمًا ذاتيًّا، أو ألا نبقي عليها سلطاننا.

(٨-٥) رد الإحراج

يكون رد الإحراج بإحدى طريقتين:
  • (أ)
    فإما أن تبين للخصم الذي يحرجك، بأن البديلين اللذين يعرضهما عليك، ويفرض أنهما الحالتان الوحيدتان المحتملتان ليستا هما الحالتين الوحيدتين، بل هناك احتمالات أخرى، وأنه يغالط حين يفترض ألا مخرج منهما؛ وعندئذٍ يسمى الرد «خروجًا من بين قرني الإحراج».١٥
  • (ب)
    وإما أن ترد الإحراج بإحراج مثله، يؤدي إلى نتيجة مناقضة لنتيجة إحراج خصمك، وعندئذٍ يسمى الرد «دفعًا للإحراج».١٦
ومن أوضح الأمثلة لدفع الإحراج، قصة تروى عن بروتاجوراس السفسطائي مع تلميذه «أواتلوس»١٧ وخلاصتها أن بروتاجوراس قد اتفق مع «أواتلوس» أن يعلمه الخطابة وطريقة المرافعة في المحاكم لقاء أجر معين، يأخذ نصفه عند فراغه من دروسه، ويأخذ النصف الثاني إذا كسب «أواتلوس» أول قضية يترافع فيها أمام المحكمة، لكن «أواتلوس» — بعد فراغه من دروسه — ماطل ولم يذهب للمرافعة أمام المحكمة هربًا من دفع القسط الثاني من أجر تعلمه؛ فرفع أستاذه بروتاجوراس عليه الدعوى للحصول على نصف أجره المؤجل، فكان دفاع الأستاذ أمام هيئة المحكمة الإحراج كالآتي:

إذا خسر أواتلوس هذه القضية وجب أن يدفع نصف الأجر المؤجل بمقتضى حكم المحكمة؛ وإذا كسبها وجب أن يدفع بمقتضى اتفاقه معي.

لكنه إما أن يخسر هذه القضية أو يكسبها.

وإذن فلا بد له في كلتا الحالتين أن يدفع القسط المؤجل.

فرد تلميذه بالإحراج الآتي:

إذا كسبت هذه القضية وجب ألا أدفع شيئًا بمقتضى حكم المحكمة؛ وإذا خسرتها، وجب ألا أدفع شيئًا بمقتضى اتفاقي مع بورتاجوراس.

لكنني إما أن أكسب القضية أو أن أخسرها.

وإذن ففي كلتا الحالتين لن أدفع له القسط المؤجل.

ومن الأمثلة التاريخية أيضًا لرد الإحراج، قصة أم أثينية مع ولدها؛ إذ أخذت تنصحه بعدم الاشتراك في السياسة محتجة له بما يأتي:

إنك في السياسة إذا قلت الصدق كرهك الناس، وإذا كذبت كرهتك الآلهة.

لكنك مضطر إما أن تقول الصدق أو أن تقول الكذب.

إذن فحتم عليك إما أن يكرهك الناس أو أن تكرهك الآلهة.

فرد عليها ابنها بما يأتي:

بل إني إذا قلت الصدق أرضيت الآلهة، وإذا قلت الكذب أرضيت الناس.

ولما كنت إما أن أقول الصدق أو أن أقول الكذب إذن فإما أن ترضى عني الآلهة، أو أن يرضى عني الناس.

١  Hypothetical Syllogism.
٢  Hypothetico Categorical Syllogism.
٣  Enthymeme.
٤  Polysyllogism.
٥  Prosyllogism.
٦  Episyllogism.
٧  Progressive.
٨  Regressive.
٩  Sorites.
١٠  هذا القياس منسوب إلى أرسطو خطأً، لأن اسمه (Sorites) لم يرد قط عند أرسطو، ولو أنه في موضع ما يشير إشارة غامضة إلى قياس من النوع الذي اصطلحنا على تسميته بهذا الاسم، وأول من عرض هذا النوع من القياس عرضًا واضحًا هم الرواقيون، والذي أطلق عليه اسمه هذا هو شيشرون.
١١  تصور مثل هذا القياس على أنه مركب من عدة أقيسة فصلت نتائجها، هو في رأينا تصور خاطئ، مصدره الظن بأن التفكير لا يكون إلا على غرار القياس ذي المقدمتين والنتيجة — كما ذهب أرسطو — والواقع أن أساس الاستدلال في أمثال هذه العمليات، هو علاقة التعدي، وعلاقة التعدي قد تطوي أي عدد من الحدود في عملية واحدة، وليس هناك أبدًا ما يبرر القول بأن العقل في مثل هذا الاستدلال المتتابع الخطوات، يقف وقفات وسطى عند الحدود الفاصلة بين قياس وقياس. راجع في ذلك ما قلناه في الفصل الثالث عشر عن نقد برادلي لمبدأ شمال القياس على ثلاثة حدود فقط وقد ذكر «وليم جيمس» أيضًا Principles of Psychology، ج٢، ص٦٤٦ نقدًا شبيهًا بهذا، قائلًا إن العملية الاستدلالية قد يكون فيها أي عدد من الحدود الوسطى، وقد نتخطى كل هذه الحدود الوسطى دفعة واحدة لتصل إلى النتيجة، وقد أطلق على هذه العملية اسم «مبدأ تخطي الحدود الوسطى Axiom of skipped intermediaries».
١٢  في الجزء الثاني من كتابه Confessio naturee contra Atheistas الذي كتبه سنة ١٦٦٨م، وهو كتاب يحتوي على نظريات خاصة بطبيعة المادة، غير أن ليبنتز عاد أخيرًا فأنكرها. وقد أخذنا المثل من Joseph، ص٣٥٥-٣٥٦.
١٣  نسبة إلى Rudolph Goclenius (١٥٤٧–١٦٢٨م).
١٤  To be on the horns of a dilemma.
وإذا شئنا الدقة، قلنا إن الإحراج لا يكون ذا «قرنين» إلا إذا كان هناك بديلان فقط، ومن ثم جاءت كلمة dilemma إذ المقطع الأول فيها di معناه «اثنان».
فإن كان هناك ثلاث بدائل، سمي الإحراج trilemma أو أربعة بدائل، سمي الإحراج tetralemma، أو أكثر من ذلك سمي Polylemma.
(راجع Welton, J. and Monahan, A. J., An Intermediate Logic، ص١٩٧).
١٥  ويسمونه بالإنجليزية Escaping through the horns.
١٦  ويسمونه بالإنجليزية Refuting a dilemma.
١٧  Euathlus.
الرجوع إلى الصفحة الرئيسية للكتاب

جميع الحقوق محفوظة لمؤسسة هنداوي © ٢٠٢٥