منطق العلاقات

(٢-١) علاقة الذاتية (الهوية)

الذاتية هي علاقة الفرد الجزئي مع نفسه، بحيث إذا اختلفت الظروف من حوله، ظل هو ما هو، ذلك إذا لم نأخذ الفرد الجزئي بالمعنى التفصيلي الدقيق، الذي يحمل الجزئي حالة واحدة من سلسلة الحالات التي من مجموعها يتكون ما جرى العُرف على تسميته بفرد جزئي؛ فالعرف يجري على أن يعتبر «العقاد» فردًا جزئيًّا؛ على حين أن الجزئي الحقيقي حالة واحدة من حالاته المتتابعة التي يتكوَّن تاريخه منها؛ لكننا لو أخذنا الجزئي بهذا المعنى الدقيق، لَمَا كان للجزئي ذاتية يحتفظ بها؛ لأن كل حالة جزئية تمضي ولا تعود، هذا المكتب الذي أمامي ليس هو على وجه الدقة المكتب الذي كان بالأمس، بل هو حالة جديدة من سلسلة حالات يتكون منها «المكتب»، هذا هو الحق الواقع، لكن الحق الواقع كذلك هو أن الحالة الجديدة التي عليها المكتب الآن، لم تغير من مكتب الأمس إلا تغييرًا طفيفًا، بحيث لا يتعذَّر على مَن رأى مكتب الأمس ثم رأى مكتب اليوم، أن يقول: إن هذا هو نفسه ذاك، أعني أنه يعرف للمكتب ذاتيته التي احتفظ بها رغم اختلاف الظروف التي تحيط به.

من أجل هذا إن إدراكنا لذاتية شيء ما مقصود به أننا رأينا الشيء في محيطين مختلفين، فعرفنا أن الشيء في هذا المحيط هو نفسه الشيء في ذلك المحيط، ولهذا أيضًا، كانت علاقتا «الذاتية» و«التباين» ضدين لا يجتمعان، بحيث إذا كان ثمة شيئان «أ» و«ب» فيستحيل أن تكون «أ» متطابقة تطابقًا ذاتيًّا مع «ب»، وفي الوقت نفسه يُقال عن «أ» إنها شيء آخر غير «ب»، إذ لو كانتا متطابقتين ذاتيًّا لما كانتا متباينتين، والعكس صحيح أيضًا، فلو كانتا متباينتين لاستحال أن تكونا متطابقتين ذاتيًّا، فالحالتان يستحيل اجتماعهما معًا، ومن ثَم أيضًا تستطيع أن تعتبر «الذاتية» و«التناقض» وجهين لحقيقة واحدة، بمعنى أن الحالتين أ، ب، إنْ كانتا متطابقتين تطابقًا ذاتيًّا، فهما ليستا بالمتناقضتين، وإن كانتا متناقضتين فيستحيل أن يكون بينهما تطابق ذاتي.

(٢-٢) علاقة التماثل^١٩

(٢-٣) علاقة التعدي^٢٣

علاقة التعدي لا بد لها من زوجين الأطراف على الأقل، بحيث يكون هنالك طرف مشترك بين الزوجين.

فإذا قلنا: إن «أ صديق ب» و«ب صديق ﺟ» أمكن أن يكون «أ صديق ﺟ» لكن يجوز ألا يكون كذلك.

أو قلنا: إن «أ تختلف عن ب» و«ب تختلف عن ﺟ» جاز الوجهان بالنسبة ﻟ «أ، ﺟ»، فقد تكون «أ» مختلفة عن «ﺟ» وقد لا تكون.

(٢-٤) علاقة الانعكاس

إن البحث الرئيسي للمنطق هو الاستدلال الصوري؛ أي إمكان اشتقاق صيغة من صيغة أخرى، وأبسط أنواع الاستدلال أن نستدل الشيء من نفسه فنقول: إن «أ يلزم عنها أ».

إذا كانت أ يلزم عنها أ، نتج أنه:

ويترتب أيضًا على كون أ يلزم عنها أ ألا يكون لترتيب المقدمات أثر في أية عملية استدلالية، أي إنه:

ويترتب على كون أ يلزم عنها أ، ثم على كون إضافة مقدمة أخرى للاستدلال الصحيح لا تفسده، ثم على كون ترتيب المقدمات غير ذي أثر في سلامة الاستدلال، أننا نستطيع من أية مجموعة من المقدمات أن نختار إحداها ونجعلها النتيجة، لأنها إن كانت صحيحة وهي مقدمة فهي صحيحة أيضًا وهي نتيجة، وصورة ذلك بالرموز كما يلي:

إنه إذا كانت العلاقة متعدية وتماثلية معًا، كانت كذلك علاقة انعكاسية، خذ مثلًا علاقة «يساوي»، فهذه يجتمع فيها التعدي والتماثل معًا، فهي متعدية لأننا من العبارتين «أ = ب» و«ب = ﺟ» نستنتج «أ = ﺟ»، وهي تماثلية لأننا من العبارة «أ = ب» نستنتج أن «ب = أ» ما دامت متعدية وتماثلية، فهي انعكاسية كذلك، أي تقوم بين الشيء ونفسه، فنقول إن أ = أ.

أما إذا اجتمع في علاقة ما التعدي واللاتماثل، كانت لا انعكاسية، مثل «أكبر من» — فهذه علاقة اجتمع فيها التعدي واللاتماثل، هي متعدية لأننا من العبارتين «أ أكبر من ب» و«ب أكبر من ﺟ» نستنتج «أ أكبر من ﺟ»، وهي لا تماثلية لأننا لا نستطيع أن نستنتج أن «ب أكبر من أ» من عبارة «أ أكبر من ب» — ما دامت متعدية ولا تماثلية، فهي لا انعكاسية أيضًا، فلا يجوز أن نقول إن أ أكبر من أ.

(٢-٥) علاقة الترابط^٣١

خذ مثلًا ثالثًا سلسلة النقط في خط مستقيم، فبين أي نقطتين تختارهما جزافًا لا بد أن تقوم علاقة «إلى يمين» وعكسها «إلى يسار» فإن كانت النقطتان هما أ، ب، وكانت «أ على يمين ب» فلا بد أن تكون «ب على يسار أ».

(٢-٦) علاقة «واحد بكثير»^٣٣

وهي علاقة تربط حدًّا واحدًا على الأكثر من ناحية بحد آخَر من ناحية أخرى، على أن هذا الحد الآخر يحتمل إحدى حالتين: فإما أن يكون هو أيضًا حدًّا وحيدًا لا يشاركه في هذه العلاقة المذكورة حد آخر، أو يكون هناك حدود غيره تشاركه فيها، والأمثلة الآتية توضح ما نريد:

فكلمة «والد» تعبر عن علاقة «واحد بكثير» بمعنى أنني إذا قلت عبارة كهذه: «أ والد ب» كانت العلاقة تربط حدًّا واحدًا على الأكثر، وهو «أ» — إذ يستحيل أن يكون للشخص ب أكثر من والد واحد — وهي تربط هذا الحد الواحد بحد آخر، هو «ب»، الذي قد يكون وحده وقد يكون معه غيره مما يرتبط مع «أ» بهذه العلاقة نفسها.

وكلمة «زوج» تعبر عن هذه العلاقة أيضًا — علاقة واحد بكثير — لأنني إذ أقول «أ زوج ب» فلا يمكن أن يكون هناك إلا حد واحد في طرف البداية من طرفَي العلاقة، أما طرف النهاية فيحتمل أن تكون «ب» هي وحدها التي ترتبط برابطة الزوجية مع «أ»، وقد يكون معها غيرها، مما يرتبط مع «أ» بهذه العلاقة نفسها.

ففي الدالة «أ والد ب»، قبل أن نحدد «قيمة» أي رمز من هذين الرمزين يكون كل فرد من أفراد الناس، ممن يجوز أن ينطبق عليه وصف كونه والدًا، «قيمة» محتملة للرمز «أ» ولذلك فمجموع «الوالدين» يؤلف ما أسميناه ﺑ «النطاق» كما أن مجموع الأفراد الذين يصح أن ينتسبوا لسواهم بعلاقة البنوة، يتكون منهم ما أسميناه ﺑ «النطاق العكسي» ومن مجموع أفراد النطاق والنطاق العكسي يتكون ما أسميناه ﺑ «المجال» الذي يجوز فيه استعمال علاقة معينة (علاقة والد في هذه الحالة التي أمامنا).

ولعل الصورة الرمزية الآتية تزيد الأمر إيضاحًا:

ففي القائمة اليمنى مجموعة الوالدين، وفي القائمة اليسرى مجموعة الأبناء، وفي القائمة الوسطى نوع العلاقة وهي «والد»، فإذا ربطنا هذه العلاقة بواحد من طائفة الأبناء، تحدَّد على وجه الدقة والحصر مَن ذا يكون طرف البداية لهذه العلاقة.

ولو قد وجدنا علاقة «والد» تربط رمزين مختلفين، «أ» و«ﺟ» بطرف واحد هو «ب»، مثل:

«أ والد ب» و«ﺟ والد ب».

مثال ذلك أن نجد العبارتين الآتيتين: «علي والد الحسين» و«ابن أبي طالب والد الحسين» فنعلم أن عليًّا هو نفسه ابن أبي طالب.

علاقة «واحد بواحد»

قلنا إن علاقة «واحد بكثير» تُحتِّم واحدية الطرف الأول، أي طرف البداية في الصيغة العلاقية، أما الطرف الثاني، وهو طرف النهاية من تلك الصيغة العلاقية، فيحتمل أحد وجهين، فإما ألا يكون هناك إلا حد واحد يمكن ربطه طرفًا ثانيًا بهذه العلاقة، أو أن يكون هناك أكثر من حد واحد؛ وإن كانت الحالة هي الأولى، سُميت العلاقة عندئذٍ علاقة «واحد بواحد».

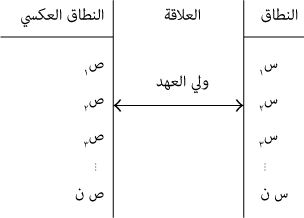
ففي علاقة «واحد بواحد» إذا حددنا طرف البداية تحدَّد بالتالي طرف النهاية، وإذا حددنا طرف النهاية تحدَّد بالتالي طرف البداية [لاحظ أننا في علاقة «واحد بكثير» إذا حددنا طرف النهاية تحدَّد بالتالي طرف البداية، لكن العكس غير صحيح، أي إننا إذا حددنا طرف البداية فلا يتحدَّد بذلك طرف النهاية]، فمثلًا العلاقة التي يدل عليها لفظ «ولي العهد» علاقة واحد بواحد؛ لأننا حين نقول: «أ ولي عهد ب»، ثم نعرف مَن هو المرموز له بالرمز «أ» نعرف بالتالي مَن يكون المرموز له بالرمز «ب»، والعكس صحيح أيضًا، أي إذا عرفنا مَن هو «ب» عرفنا بالتالي مَن ذا يكون «أ».

إذا ربطنا حدود طائفتين، بحيث نجد لكل حد من طائفة ما يقابله من حدود بالطائفة الأخرى، كانت الطائفتان مرتبطتين بعلاقة «واحد بواحد»، «فإذا فرضنا أن العالم يخلو خلوًّا تامًّا من تعدد الزوجات للزوج الواحد، ومن تعدد الأزواج للزوجة الواحدة، بحيث أصبح لكل زوج زوجة واحدة، ولكل زوجة زوج واحد، فواضح أن عدد الأزواج في أية لحظة سيكون هو نفسه عدد الزوجات؛ ولسنا بحاجة عندئذٍ إلى إحصاء ليؤكد لنا هذه الحقيقة، كلا ولا نحن بحاجة في ذلك إلى معرفة العدد الحقيقي للأزواج والزوجات، وإنما نعرف أن العدد في كل مجموعة يساوي العدد في المجموعة الأخرى، ما دام لكل زوج زوجة واحدة ولكل زوجة زوج واحد، عندئذٍ تكون العلاقة بين الأزواج والزوجات علاقة واحد بواحد.»^٣٨

وواضح من هذا المثل السابق، أن عملية العد إنْ هي إلا ربط طائفتين بعلاقة «واحد بواحد»، طائفة الأعداد من جهة وطائفة المعدودات من جهة أخرى، فإذا عددت برتقالات ووجدتها خمسًا، كان ما فعلته هو أني ربطت كل برتقالة بعدد من سلسلة الأعداد، على الصورة الآتية:

برتقالة_١ برتقالة_٢ برتقالة_٣ برتقالة_٤ برتقالة_٥.

ولذا كانت عملية العد باطلة إذا رقمت برتقالتين مثلًا بعدد واحد، أو إذا رقمت برتقالة واحدة بعددين.

وعلى هذا الأساس تكون العلاقة بين الجنود وأرقامهم، أو بين أصحاب السيارات وأرقام السيارات، أو بين أصحاب أجهزة التليفون وأرقام تلك الأجهزة علاقة «واحد بواحد»؛ بحيث إذا عرفت حدًّا في أحد النطاقين، عرفت بالتالي الحد الذي يقابله في النطاق الآخر.

وكذلك علاقة «التشابه» بين شيئين، هي في حقيقتها علاقة، «واحد بواحد» بينهما، بحيث أجد لكل عنصر من عناصر الشيء الأول ما يقابله من عناصر الشيء الثاني، على شرط ألَّا يكون هنالك في أحد الشيئين أكثر من عنصر واحد مقابل لعنصر واحد في الشيء الثاني، فأقول مثلًا عن أسرتين إنهما شبيهتان في التكوين، إذا كانت العلاقة بين أفرادهما هي علاقة «واحد بواحد» فوالد يقابل والدًا، ووالدة تقابل والدة، وابن أكبر يقابل ابنًا أكبر، وبنت صغرى تقابل بنتًا صغرى.

والقضية التي تصف شيئًا في الطبيعة، تحتوي على عدد من الحدود يقابل عناصر الشيء الموصوف مقابلة تامة، أي يكون بين النطاقين علاقة «واحد بواحد»، مثل قولي: «الطائر على الشجرة»، فكلمة «طائر» تقابل طائرًا، وكلمة «شجرة» تقابل شجرة، وكلمة «على» تقابل العلاقة بينهما.

وفي كل تصوير صادق، يكون بين الصورة وأصلها علاقة «واحد بواحد» كالخريطة الجغرافية والإقليم الذي تصوره، والرسوم التخطيطية لمدينة أو لمنزل، وهكذا؛ ولعل الصورة الرمزية الآتية توضح ما نريد (في قولنا) س ولي:

أي إننا إذا حددنا س_٢ من أفراد النطاق على أنه ولي عهد فلان، كان فلان هذا هو على التحديد ص_٢ من أفراد النطاق العكسي، وإذا حددنا ص_٢ من أفراد النطاق العكسي على أنه يولي العهد لفلان، كان فلان هذا هو على التحديد س_٢ من أفراد النطاق.

(٢-٧) اندماج العلاقات

قد تندمج علاقتان في علاقة واحدة، وهو ما يُسمى بعملية الضرب في العلاقات لأنها شبيهة بعملية الضرب في الحساب، وتُسمى العلاقة التي نحصل عليها بهذه العملية بحاصلي ضرب العلاقتَين.

خُذ لذلك مثلًا يوضح المراد: علاقة العمة بابن أخيها، هي في الحقيقة حاصل ضرب علاقتين، هما: (١) علاقة الأخت بأخيها. (٢) علاقة الوالد بابنه.

فلو رمزنا بالرموز لعلاقة الأخت بأخيها، بحيث يكون معنى العبارة الآتية: «أ ع ب» هو «أ أخت ب»، ثم لو رمزنا بالرمز س لعلاقة الوالد بابنه أو بنته، بحيث يكون معنى العبارة الآتية: «ب س د» هو «ب والد د»، كانت العلاقة بين «أ» و«د» هي حاصل ضرب العلاقتين ع، س ويرمز لعملية الضرب بين العلاقات بخط عمودي هكذا «/»، فإذا كتبنا هذه العبارة «ع/س» كان معناها «اندماج العلاقتين ع، س في علاقة واحدة».

على أن العلاقتين المضروبتين إحداهما في الأخرى، بحيث تندمجان في علاقة واحدة تجمعهما معًا، لا تقبلان الرجوع، أي إنهما لا تكونان معًا علاقة تماثلية؛ ففي قولنا «أ أخت ب» و«ب والد ﺟ» إذَن «أ عمة ﺟ» لا يمكن قراءة العلاقتين في اتجاه عكسي لتنتجا النتيجة عينها؛ إذ لو قلنا: «ﺟ والد ب» و«ب أخت أ» كانت النتيجة أن «ﺟ والد أ».