العلم الصوري وعلم الواقع
١
-
(أ)
رموزًا منطقية وهي التي تؤدي في الجملة أو في الصيغة الرمزية مهمة ربط الأجزاء في وحدة معينة، دون أن يكون لها هي بذاتها دلالة في عالم الأشياء؛ مثل «أو» و«ليس» و«كل» و«إذا» و«٣» و«+».
-
(ب)
رموزًا وصفية (أو شيئية) وهي التي تستخدم لتشير إلى مسميات في عالم الأشياء الفعلية، مثل «ماء» و«حديد» و«القاهرة».
- (أ) فكل عبارة لا تشتمل إلا على رموز منطقية فقط تكون جملة مقطوعًا بها — فهي إما مقطوع بصوابها أو مقطوع ببطلانها — وإذا وصفنا عبارة بقولنا إنها «جملة منطقية» كان المراد هو أنها جملة لا تشتمل إلا على رموز منطقية فالجملة المنطقية نوعان:
- (١)
جملة تحليلية، وذلك حين يكون صدقها صدقًا مطلقًا، نقرره لها بناءً على طريقة بنائها وحدها، دون النظر إلى أي شيء في العالم الواقع، وبغض النظر عن صدق أو كذب أية جملة سواها؛ ومن قبيل ذلك قولنا: («أ» أو «لا − أ») وقولنا: («أ» هي «أ»).
- (٢)
جملة متناقضة، وذلك حين يكون بطلانها بطلانًا مطلقًا، نقرره عنها بناءً على طريقة بنائها وحدها، دون النظر إلى أي شيء في العالم الواقع، وبغض النظر عن صدق أو كذب أية جملة سواها؛ مثل قولنا: («أ» و«لا − أ»).
- (١)
- (ب) وأما النوع الثاني من العبارات فهو الجمل الوصفية وأعني بها الحالات التي تشتمل فيها الجملة على كلمة وصفية (شيئية) واحدة على الأقل، أي إنها لا تقتصر على الرموز المنطقية وحدها، مثل قولنا: «إما أن تكون شيكاغو واقعة على نهر الهدسن أو لا تكون» وقولنا: «الرصاص ينصهر في درجة ٣٣٠ مئوية» ومن ذلك نرى أن الجملة الوصفية إما أن تكون:
- (١)
تحليلية، وذلك حين يكون بناء الجملة وحده كافيًا للدلالة على صدقها. كقولنا «إما أن تكون شيكاغو واقعة على نهر الهدسن أو لا تكون» وكقولنا «عدد سكان القاهرة لا يكون زوجيًّا وفرديًّا في آنٍ واحد».
- (٢)
أو تركيبية، وذلك حين تكون لا هي تحليلية فيقطع بصوابها ولا هي متناقضة فيقطع ببطلانها، لكنها تحتاج إلى مراجعتها على الواقع لنعلم إن كانت صادقة أو باطلة؛ وذلك كقولنا «نهر النيل أطول من نهر الكونجو»، فليس في بناء الجملة نفسه هنا ما يدل على أنها صواب ولا ما يدل على أنها خطأ، بل الأمر مرهون بمطابقتها أو عدم مطابقتها للواقع الخارجي.
- (١)
ونعود إلى تقسيم العلوم نوعين: علوم صورية وعلوم عن الواقع؛ فأما العلوم الصورية فهي التي لا تشتمل إلا على جمل تحليلية، وهي التي يدل بناؤها اللفظي وحده على صدقها؛ وهذه الجمل التحليلية إما أن تكون مقتصرة على رموز منطقية فقط، وإما أن ترد فيها رموز وصفية (أي مشيرة إلى أشياء) لكن بناءها وحده — رغم ذلك — يكون دالًّا على صدقها.
- (١)
جملة تحليلية وصفية وهي المشتملة على رمُوز ليست منطقية (كأسماء الأشياء) إلا أنها تحتوي على هذه الرموز اللامنطقية بصورة تمكننا من الحكم عليها بالصدق أو بالبطلان، لمجرد طريقة بنائها، وبغض النظر عن دلالات الرموز الداخلة في تكونيها، كقولنا: «إما أن تكون جبال الهملايا في آسيا أو لا تكون».
- (٢) جملة تحليلية منطقية، وهذه قسمان:
- (أ)
جملة تحليلية منطقية بالمعنى الضيق لكلمة «منطقية»، وهي التي لا تشتمل إلا على رموز مما جرى العرف على أنها داخلة في مجال علم المنطق.
- (ب)
جملة تحليلية منطقية بالمعنى الواسع لكلمة «منطقية» وعندئذٍ تشمل مجال الرياضة بالإضافة إلى مجال المنطق.
- (أ)
على أن علوم الواقع إذ تشتمل على جمل تركيبية وجمل تحليلية بنوعيها السالفين، فإنما تستخدم الجمل التركيبية لغرض والجمل التحليلية لغرض آخر؛ فهي تستخدم الجمل التركيبية لتصف بها الوقائع المشاهدة، كأن يصف العالِم الطبيعي — مثلًا — ما يحدث في معمله إبان قيامه بالتجارب التي يجريها، وكأن يصف الجغرافيُّ ما يشاهده إبان ارتياده مكانًا كان مجهولًا؛ لكن رجال العلم هؤلاء لا يكتفون بمجرد تسجيلهم لما يشاهدونه أثناء قيامهم ببحوثهم، بل هم في نهاية هذه المشاهدات يحاولون أن يصوغوا «فروضًا» ليفسروا بها الظواهر التي هي موضع بحوثهم؛ وبطبيعة الحال لا تجيء هذه الفروض على صورة الوصف الجزئي لحادثة مفردة، بل تجيء على صورة صيغة عامة لتصلح أن تكون قانونًا ينطبق على كل الحالات التي تنتمي إلى ظاهرة بعينها؛ وهذه الصياغات العامة هي أيضًا من قبيل الجمل التركيبية في بناء علوم الواقع.
هكذا ترى أننا بالخطوات الصورية (من منطق ورياضة) لا نضيف مادة جديدة إلى مادة البحث، لكننا نستعين بها على الانتقال مما عندنا إلى ما ليس عندنا من معلومات مما كان متضمنًا في معلوماتنا الأولى، فأصبح الآن معلومًا لنا علمًا صريحًا.
وفيما يلي جدول يبين ما قد أسلفناه من أنواع الجمل وأنواع العلوم، وهو من وضع رودلف كارناب.
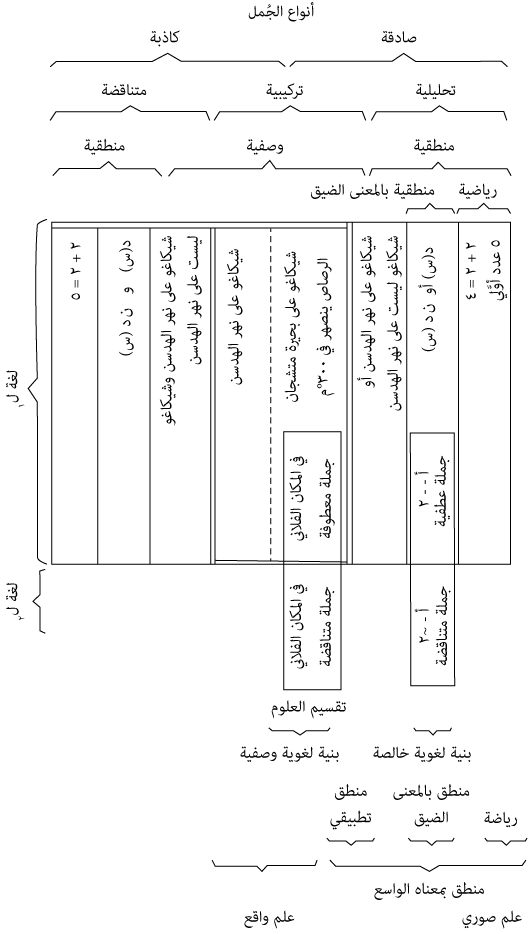
وها نحن أولاء نحلل لك محتوى الجدول لأهميته في تلخيص منطق العلوم تلخيصًا مركَّزًا ولكنه شامل.
فهو يقسم الجمل إلى صادقة وكاذبة، وهنا نلاحظ أن الجملة التي لا تصلح لأن توصف بصدق أو بكذب تكون جملة خارجة عن نطاق المنطق، أي إنها خارجة عن مجال العلوم، كالعبارات التي يعبر بها أصحابها عن حالاتهم الوجدانية مثلًا.
أما الجمل الصادقة فهي إما تحليلية أو تركيبية، وأما الجمل الكاذبة فهي إما تركيبية أو متناقضة؛ ومعنى ذلك أن الجملة إذ تكون صادقة فإنما يعتمد صدقها هذا إما على طريقة بنائها الرمزي نفسه — ومن قبيل ذلك المنطق والرياضة — كقولنا «أ = أ» وقولنا «سكان القاهرة إما يقلون عن ثلاثة ملايين نسمة أو يزيدون على ثلاثة ملايين نسمة أو يساوون ثلاثة ملايين نسمة» ففي مثل هذه الحالات نحكم بالصدق بمجرد النظر في طريقة البناء اللفظي، أو يعتمد صدق الجملة الصادقة لا على مجرد بنائها اللفظي، بل على مطابقة صورتها اللفظية لصورة الواقعة الخارجية التي جاءت الجملة لتصفها.
والجملة إذ تكون كاذبة، فإنما يجيء كذبها هذا إما من ناحيتها الوصفية، بمعنى أنها تدَّعي وصف الواقع الخارجي مع أنها لا تطابقه، أو يجيء كذبها نتيجة لتركيبها اللفظي نفسه، وذلك إذ يشتمل هذا التركيب على رموز متناقضة، كأن نقول مثلًا: «إن طنطا شمالي القاهرة وليست شماليها».
- (١)
الجملة التحليلية تكون إما منطقية وإما وصفية؛ أعني أنها إما أن تكون مقتصرة على رموز منطقية فقط، أو أن تكون مشتملة على كلمة شيئية واحدة على الأقل تربط الصلة بينها وبين الواقع.
فإن كانت منطقية كانت إما رياضية مثل قولنا ٢ + ٢ = ٤، أو كانت منطقية بالمعنى الضيق لهذه الكلمة كقولنا: («أ» إما أن تكون «س» أو «لا − س»).
وأما إن كانت الجملة التحليلية وصفية، كانت مشتملة على كلمات شيئية وكانت في الوقت نفسه دالة على صدقها بمجرد الطريقة التي صيغت بها كلماتها، مثل: «إما أن تكون شيكاغو واقعة على نهر الهدسن أو غير واقعة على نهر الهدسن».
- (٢)
الجملة التركيبية الصادقة لا تكون إلا وصفية تصف الواقعة التي جاءت لتصفها وصفًا صحيحًا، كقولنا: «شيكاغو على شاطئ بحيرة ميشجان» وقولنا: «الرصاص ينصهر في درجة حرارة ٣٣٠ مئوية».
ويلاحظ أنه من هذا القبيل نفسه أن يقول القائل عن جملة ما وردت في مكان ما من كتاب معين مثلًا: هنالك في ذلك الموضع المعين جملة عطفية؛ فعندئذٍ تكون العبارة تركيبية وصفية تتحقق بالرجوع إلى الواقع بنفس الطريقة التي تتحقق بها عبارة تتحدث عن مدينة شيكاغو أو نهر النيل.
إلى هنا انتهينا من أقسام الجملة الصادقة؛ وننتقل إلى الجملة الكاذبة فنقول إنها تجيء على إحدى الصور الآتية:
١- فهي إما تركيبية كاذبة، أي إنها جاءت زاعمة أنها تصف واقعة ما، لكن زعمها باطل، لأنها لا تطابق الواقعة التي جاءت لتصفها، كقولنا: «شيكاغو على نهر الهدسن» (مع أن شيكاغو في الحقيقة على شاطئ بحيرة ميشجان).
أو هي متناقضة، فليس كذبها نتيجة لعدم مطابقتها للواقع فحسب، بل إن رموزها نفسها يناقض بعضها بعضًا حتى ليحكم الإنسان عليها بالبطلان بغير رجوع إلى الواقع؛ وهذا التناقض يتخذ إحدى صورتين:
(أ) فهو إما تناقض في جملة وصفية كقولنا: «شيكاغو واقعة على الهدسن وليست واقعة على الهدسن»؛ أو هو تناقض في جملة منطقية كقولنا: «أ هي س ولا − س معًا».
- (١)
صورية، وتشمل الرياضة، والمنطق بمعناه الضيق، والمنطق التطبيقي.
فالرياضة هي الجمل الصادقة، التحليلية، المنطقية، مثل «٢ + ٢ = ٤»، و«٥ عدد أولي».
والمنطق بمعناه الضيق هو الجمل الصادقة، التحليلية، المنطقية، المقتصرة على مصطلحات المنطق كما جرى به العرف، مثل «أ ~ ⋅ أ جملة عطفية» (أي أ ولا − أ جملة عطفية). لاحظ أنه لا فرق بين الرياضة والمنطق إلا بما نصطلح عليه من حيث سعة المجال ليشمل الأعداد أو ضيقه لتخرج منه الأعداد، وهو اصطلاح جزافي صرف لأن الجوهر واحد فيما يسميه العرف منطقًا وما يسميه رياضة.والمنطق التطبيقي هو الجمل الصادقة، التحليلية، الوصفية مثل «شيكاغو واقعة على الهدسن أو غير واقعة على الهدسن».
- (٢)
أو قد تكون العلوم واقعية وهي تشمل الجمل التركيبية الوصفية (لاحظ أن الجملة التركيبية قد تكون منطقية لا وصفية، كقولنا «إما أن تكون شيكاغو على الهدسن أو ليست على الهدسن» وعندئذٍ تندرج تحت العلوم الصورية).
٢
ونقصر حديثنا الآن على قضايا العلم الصوري، لنعود بعد فراغنا منها فنتناول قضايا علم الواقع، كي تتبين المقارنة بينهما واضحة؛ فإذا ما وجدنا أنفسنا أمام موقف مشكل، وعرض لنا فرض ما باعتباره طريقًا ممكنًا للحل، مَثُلَ هذا الفرض أمام أذهاننا في صورة قضية (اللهم إلا إذا قبلناه فورًا وصدقناه ثم طبقناه على الموقف المشكل، وعندئذٍ لا تكون قضايا ولا يكون بحثٌ علمي) لكن هذه القضية التي ستضع الحل الممكن للمشكلة المائلة أمام العقل، سرعان ما يتبين أنها ليست قائمة في الفراغ وحدها، بل إنها لترتبط مع عدد غيرها من الأفكار التي كان قد سبق لنا تحصيلها وتحقيقها في مجرى حياتنا الماضية، فإذا ما ربطنا هذه القضية الجديدة بزميلاتها القدامى، راعينا في الربط أن نلتمس لها مكانًا في نسق يشملها ويشمل تلك الزميلات شمولًا يمكننا من استنباط أجزاء النسق بعضها من بعض، استنباطًا نظل نسير فيه داخل عقولنا خطوة بعد خطوة، فمن مقدمة إلى نتيجة، ومن هذه النتيجة إلى نتيجة تلزم عنها، وهكذا نسير في تسلسل لا نخبط به خبط الأعشى، بل نتجه به وجهة نتصور أنها قد تنتهي بها آخر الأمر إلى نتيجة ربما وجدناها تحل المشكلة التي كانت عرضت لنا بادئ ذي بدء.
وإذا قلنا إن القضية التالية تكون «مساوية في قوتها المنطقية» للقضية الأولى، فلسنا نريد بذلك أنها تكون مجرد «تحصيلًا للحاصل»، إذ إن «تعادل» القضايا ليس هو بذاته «تحصيل الحاصل» إلا إذا فهمنا عبارة «تحصيل الحاصل» بمعنى اصطلاحي خاص يسوِّي بينه وبين «التعادل» المقصود؛ والمعنى المقصود بالتعادل هو أن تجيء القضايا الأخيرة في تسلسل التفكير بحيث تكون هي نفسها القضايا الأولى في ذلك التسلسل، لا من حيث «المضمونات» بل من حيث القوة الإجرائية؛ فالمضمونات تختلف في كل خطوة عنها في الخطوة التي سبقتها، لكن تبقى القوة الإجرائية واحدة في كلتا الخطوتين؛ ومن ثم يجيء مبدأ «الاتجاه» الذي لا بد أن نسير فيه أثناء البحث لكي ينتج، فنحن إذ ننتقل من مضمون فكري إلى مضمون فكري آخر يختلف عنه مادة ولكنه يتساوى معه إجراء، نتخير من المضمونات الكثيرة المختلفة في مادتها ولكنها متساوية في قواها الإجرائية، ما عساه أن ينقلنا نحو نتيجة يمكن الانتفاع بها في التطبيق الفعلي على المشكلة القائمة تطبيقًا لم يكن مستطاعًا ونحن بعدُ بإزاء مضمونات القضايا الأولى؛ فاختلاف المضمونات الفكرية في آخر الشوط الفكري النظريِّ عنها في أوله، هو الذي لا يجعل الآخر تحصيلًا للحاصل بالنسبة للأول، إلا إذا كان المقصود هو تساوي «القوة الإجرائية» في الحالتين، لا تساوي المضمونات تساويًا ذاتيًّا، بالمعنى الذي يجعل الحالتين حالة واحدة مكررة في صورتين لغويتين مترادفتين.
خذ مثلًا لذلك فكرة «التيار الكهربي» وفكرة «المقاومة» فالمعادن تختلف في قابليتها لتوصيل التيار وفي مقاومته؛ فإذا عرف الباحث أن فكرة «التيار الكهربي» مساوية من حيث القوة الإجرائية لفكرة «فرق الجهد مقسومًا على المقاومة» بحيث استطاع أن ينتقل من مضمون الفكرة الأولى إلى مضمون الفكرة الثانية، كان بذلك يستبدل بفكرة لم يكن يعرف كيف يستخدمها في حل مشكلة يراد حلها، فكرة أخرى مختلفة عنها مضمونًا، ومساوية لها إجراء، ويعرف كيف يستخدمها في التطبيق العملي على ما هو ماثل أمامه من مشكلات الوجود الفعلي؛ وها هنا تكمن قدرة الباحث العلمي، فليس الأمر مقصورًا على انتقال لفظي بين «مترادفات» بل إنه إدراك للتساوي في قوة الإجراء الفعلي بين أفكار كانت تبدو وكأنها متباينة إلى الحد الذي لا تستقيم معه في نسق فكري واحد.
وننتقل الآن إلى قضايا الواقع لنبين مواضع الاختلاف بينها وبين قضايا الاستنباط الصوري؛ فأنت إذا كنت بصدد موقف معين تريد أن تصفه وصفًا يحدد فيه موضوع المشكلة المراد حلها، أخذت تتخير جوانب معينة من ذلك الموقف لتسوق كل جانب منها في قضية تصوره، بحيث يتكون من مجموعة القضايا صورة متكاملة لما تريد تصويره؛ فكل قضية هنا مستقلة وغير معتمدة على أخواتها، وإن تكن متعاونة معها على بناء صورة واحدة؛ وما أشبه ذلك بالشهود في المحكمة، فكل شاهد يصف جوانب الموقف كما رآها، وعلى القاضي أن يجمع هذه الأقوال جمعًا يكون منه موقفًا متماسكًا، فها هنا لا تكون شهادة أحد الشهود «مستنبطة» من شهادة شاهد آخر، ولا هي لازمة عنها بأي معنى من المعاني، بل يجيء كل منها مستقلًّا، وربما تناولت إحداهما جانبًا من الموقف غير الجانب الذي تناولته الأخرى.
وهكذا قل في مجموعة القضايا التي يسوقها الباحث وصفًا للموقف الماثل أمامه؛ مثال ذلك الطبيبُ في تشخيصه للمرضى، تراه يقوم بإجراءات مستقل بعضها عن بعض، تزوده بمعلومات أولية منوعة، فيعلم منه درجة الحرارة، والنبض، والتنفس، وإفراز الكليتين، وحالة الدم … إلخ، وربما بحث في العناصر الموروثة في مريضه؛ وهكذا يمضي في جمع معلومات مستقلة بعضها عن بعض، ولا يجمع بينها إلا التقاؤها كلها في الدلالة، إذ قد يقوِّي بعضها بعضًا في الدلالة على أن المريض مصاب بكذا وكذا؛ فلو أخذنا القضايا التي سبقت فيها تلك المعلومات واحدة بعد واحدة، ألفيناها ذات قوة دلالية في بيان طبيعة المرض وفي الإيحاء بطريقة العلاج الممكن، وإذا تجمعت فإن قوة الواحدة منها تزيد من قوة الأخرى.
والعلاقة المتبادلة بين الجانب الصوري النظري في التفكير وبين الجانب الوصفي التطبيقي، واضحة؛ فأولًا لا يمكن البدء في شوط التفكير النظري إلا من بداية توحي بها مشاهدة الواقع، لأن مشاهدة المشكلة القائمة أمامنا في العالم الخارجي هي التي توحي بطريقة حلها، فنضع أمام الأذهان هذا الفرض الموحى به، ونترك الواقع مؤقتًا، لنأخذ في استبدال نظري ننتقل به من فكرة إلى فكرة مساوية لها في قوة الإجراء وإن اختلفت معها في مادة المضمون، حتى ننتهي في سلسلة الاستبدالات الفكرية إلى نتيجة يخيل إلينا أنها قد تكون فعالة في علاج المشكلة القائمة في الموقف الخارجي، فعندئذٍ نخرج بتلك النتيجة إلى التطبيق لنرى مدى توفيقها في ذلك.
وهنا نقطة منهجية هامة لا بد من ذكرها في هذا الموضع، وهي أننا عندما نخرج بالنتيجة النظرية إلى الواقع الفعلي، فإما أن نجدها قابلة للتطبيق على ذلك الواقع أو غير قابلة، فإن كانت غير قابلة للتطبيق، أعني أن الواقع يكذبها، كان لا مناص من نبذ الفرض الذي كانت تلك الفكرة قد بنيت عليه في الاستنباط النظري؛ وأما إن وجدناها قابلة للتطبيق على الواقع، أعني أن الواقع يؤديها، لم يكن معنى ذلك أنها فكرة صادقة حتمًا، وكل ما في الأمر أن درجة احتمال صدقها تزداد إلى أن تجيء شواهد أخرى من الواقع تزيد من تأييدها، وهكذا تظل درجة التأييد في الزيادة دون أن نبلغ منه درجة اليقين الكامل.
إن لهذه الحقيقة أهمية منهجية كبيرة، فكثيرًا ما حدث في تاريخ العلوم الطبيعية أن ظُنَّ الصدق بنظرية ما حين وُجِدَ بعض نتائجها محققًا على الواقع، على حين أن هذه النتائج نفسها يجوز أن تنتج عن نظرية أخرى معارضة ما، لاشتراك النظريتين في بعض جوانبهما، وإن لم يكونا متطابقتين تمامًا؛ فلا استحالة — والحالة هذه — أن تكون النتائج التطبيقية التي وجدناها على الواقع، ناشئة عن الجوانب المشتركة بين النظريتين، وإذن فهي وحدها لا تصلح إثباتًا لإحداهما دون الأخرى، ولا بد من المضي في جمع الشواهد حتى نمس بها الجوانب غير المشتركة بين النظريتين، فعندئذٍ فقط نستطيع رد النتائج السالفة الذكر إلى هذه أو تلك من النظريتين.
فالهندسة الإقليدية والهندسة اللاإقليدية مشتركتان في جوانب ومختلفتان في جوانب أخرى؛ وكلنا يعلم كيف أن انطباق هندسة إقليدس على الأسطح والخطوط التي تقع لنا في عالمنا الأرضي انطباقًا لا يتخلف أبدًا، قد اتخذ فيما مضى دليلًا يقضي بأن تكون تلك الهندسة لا يقتصر صدقها على جانبها الصوري وحده، بل إنها تصدق كذلك على الواقع، مما حدا بكثير من الفلاسفة (وعلى رأسهم كانْت) أن يصبَّ بحثه الفلسفي كله على هذا التطابق بين ما ينتهي إليه العقل النظري من نتائج، وبين ما تصادفه التجربة العملية من وقائع؛ والغلطة هنا هي ما قد أشرنا إليه، وهو أن انطباق نتائج النظرية على حالات الواقع لا يكفي وحده دليلًا على صدق النظرية بالنسبة إلى الواقع، لأن تلك النتائج قد تكون تابعة لنظرية أخرى مشتركة مع النظرية الأولى في بعض الجوانب التي كان من شأنها أن تولدت تلك النتائج؛ ولو قلنا ذلك بلغة منطقية اصطلاحية مختصرة، فإننا نقول: إن إثبات التالي في القضية الشرطية لا يستتبع بالضرورة إثبات المقدَّم.
٣
ركن أساسي من أركان الفكر الرياضي أن تكون مفاهيم النسق الرياضي الواحد ممكنة التحويل بعضها إلى بعض؛ فلقد أسلفنا القول في الفقرة الماضية بأنه إذا ما واجه الباحث موقفًا مشكلًا وأراد أن يفض إشكاله، فكثيرًا ما يوحي إليه الموقف نفسه بفكرة لحله، فيأخذ الباحث عندئذٍ في تحوير هذه الفكرة داخل رأسه تحويرًا ينتقل فيه من قضية إلى قضية أخرى تلزم عنها، ومن هذه إلى ثالثة فرابعة حتى ينتهي إلى مضمون فكري يرى فيه أنه قد يكون هو الأداة المباشرة لحل الإشكال في الموقف الخارجي إذا ما طُبِّقَ على الوجود الفعلي؛ ورأينا فيما مضى كذلك أن سُلَّم القضايا الذي ننتقل عليه من بداية الشوط إلى نهايته يكون مسلسلة، ولا يكون مجرد مجموعة أفرادها مستقلة كما هي الحال في جمع الشواهد من المشاهدات الخارجية؛ فكل قضية في تلك المسلسلة تكون «لازمة» عن التي سبقتها، وقد شرحنا «اللزوم» في هذه الحالة بأنه «تعادل» بين القضيتين: السابقة واللاحقة، وهو تعادل من حيث القوة الإجرائية لكل منهما، وليس هو تعادلًا في مضمونهما؛ فقد تكون قضية منهما عن «الحركة» وقد تكون قضية أخرى عن «الحرارة» لكن الجانب الأدائي للأولى هو نفسه الجانب الأدائي للثانية، فتؤدي بالثانية في الواقع الخارجي ما تؤديه بالأولى.
وما دامت قضايا المسلسلة العقلية متعادلة بالمعنى المذكور، فهي إذن ممكنة التحويل بعضها إلى بعض، فَلَكَ أن تُحِلَّ أيَّها محل أيِّها؛ ويستحيل أن تتكسب المفاهيم هذه الخاصية إلا إذا صيغت كلها صياغة علمية كمية تُظهر ما بينها من تعادل، أما إذا تركت في صورتها التي تجري بها في مجرى التفاهم بين الناس في شئون حياتهم اليومية، فعندئذٍ لا يكون ثمة من سبيل لإدراك التعادل بينها، ذلك التعادل الذي يمكننا من إحلال بعضها محل بعض كما نشاء، فإذا كان كل مفهوم منها هو عبارة عن حالة «ممكنة» من حالات الوجود الفعلي، كان تسلسل المفاهيم في تفكيرنا الرياضي معناه الانتقال من حالة «ممكنة» إلى حالة «ممكنة» أخرى من حالات الوجود الفعلي؛ وهذه «الإمكانات» الكثيرة تصاغ في رموز رياضية فتكون هي المعادلات الرياضية التي نظل ننتقل فيها من معادلة إلى معادلة حتى نرسو آخر الأمر على معادلة نلمح فيها أنها مُيَسَّرة التطبيق المباشر على الوجود الخارجي؛ وبهذا يكون تفكيرنا الرياضي متحررًا من قيود الواقع الفعلي، لكنه في الوقت نفسه يستهدف الوصول إلى مرحلة يكون فيها التطبيق على الواقع أمرًا ميسورًا؛ على أن الجانب الرياضي من تلك المفاهيم المتعادلة في النسق الواحد، ليس هو في مضمونات تلك المفاهيم، لكنه قائم في العلاقات الضرورية التي ترتبط بها تلك المفاهيم بعضها ببعض؛ ففي قولنا إن «٢ + ٢ = ٤» مثلًا ربط بين مفهومين هما: مفهوم ٢ ومفهوم ٤، بغض النظر عن مضمون كل من هذين المفهومين، إذ جانب الرياضة في الأمر هو أن أعلم أن المفهوم الأول لو أُجْرِي عليه التكرار مرتين لصار متعادلًا مع المفهوم الثاني.
والذي يهمنا في هذا الفصل هو بيان العلاقة بين العلم الصوري وعلم الواقع — بين الرياضة من جهة والعلوم الطبيعية من جهة أخرى — ففضلًا عن أن الفرض أو مجموعة الفروض التي نفرضها لتفسير العالم الخارجيِّ وحلِّ مشكلاته تُدْرَس في العقل دراسة رياضية، بمعنى أننا نحاول استخراج ما يلزم عنها من نتائج، أعني أننا نحاول العثور على ما يساويها بين المفاهيم الأخرى من الناحية الأدائية، بعيدًا عن صدق تلك الفروض والمفاهيم أو عدم صدقها من الناحية المادية، مما يجعلها في صورتها المجردة تلك قابلة لأكثر من تطبيق مادي واحد، لأنها عندئذٍ تكون كأنها الأواني الفارغة مستعدة أن تُملأ بأية مادة صالحة لملئها، أقول إنه فضلًا عن ذلك فإن دراسة الصور الرياضية على هذا النحو المجرد تعيننا على استكشاف العامل الثابت أو الجانب المطرد الوقوع في المواقف الفعلية المختلفة التي تعرض لنا في مجرى التجربة الحسية؛ فألوف الأجسام المادية تسقط في عالَم الحسِّ: ماء النهر، وقطرات المطر، وقذائف المدافع، والأحجار الملقاة … إلخ، إلخ، وهي كلها مواقف تختلف في تفصيلاتها، لكن بينها جانبًا مشتركًا ثابتًا مطردًا، هو نفسه الجانب الذي تظهره الصيغة الرياضية التي نصوغ بها قانون الجاذبية.
فبين القانون الرياضي وبين الواقعة الحسية التي ينطبق عليها ذلك القانون موازاة في طريقة البناء أو صورة التركيب، وغاية ما في الأمر أن القانون الرياضي يقدم هذا البناء هيكلًا فارغًا من المادة، وأما الواقعة المعينة فتقدمه مليئًا بمادة متعيِّنة؛ وجدير بنا في هذا الموضع من سياق الحديث أن نوضح فكرة الموازاة هذه لبالغ أهميتها في فهم العلاقة بين الرياضة والعلوم الطبيعية:
يقال عن بنائين — أو أكثر — إنهما متوازيان أو متناظران إذا كان بينهما علاقة واحد بواحد في شبكة العلاقات التي تكون البنية في كل منهما.
والحقيقة الرياضية وكل ما يساويها من حقائق رياضية هي بمثابة بناءات هيكلية يوازي بعضها بعضًا من جهة، ثم قد نجد من وقائع الطبيعة الخارجية ما يكون أيضًا موازيًا لها في طريقة البناء، فإن وجدنا، كانت تلك الصورة الرياضية هي القانون الصوري الذي ينتظم هذه الواقعة الطبيعية وكل ما جرى مجراها من وقائع، وإلا بقيت تلك الصورة الرياضية صورة بغير تطبيق؛ فقانون الجاذبية صورة رياضية تلبس عدة ظواهر طبيعية تبدو وكأنما هي مختلفة، ولا ينبهنا إلى كونها مظاهر لحقيقة طبيعية واحدة إلا أن صورة رياضية واحدة تلبسها جميعًا على حد سواء، فقانون الجاذبية ينطبق على حركة الكواكب انطباقه على أرجحة البندول، وعلى سقوط قطرة الماء أو سقوط قطعة من الحجر.
بناء (١)
مجموعة البديهيات
- بديهية ١: إذا كان هنالك مجموعة ما «س» وكانت «أ» و«ب» عضوين في هذه المجموعة، كان هنالك على الأقل فئة فرعية واحدة مشتملة على أ، ب معًا.
- بديهية ٢: إذا كانت «أ» و«ب» فردين متميزين من أفراد «س»، لم يكن هناك أكثر من فئة فرعية واحدة مشتملة على أ، ب معا.
- بديهية ٣: أي فئتين فرعيتين في المجموعة «س» فيهما على الأقل عضو واحد مشترك بينهما.
- بديهية ٤: هنالك في المجموعة «س» فئة فرعية واحدة على الأقل.
- بديهية ٥: كل فئة فرعية تشتمل على ثلاثة أفراد — على الأقل — من أفراد المجموعة «س».
- بديهية ٦: أعضاء المجموعة «س» لا تنتمي كلها إلى فئة فرعية واحدة.
- بديهية ٧: ليس هناك فئة فرعية تشتمل على أكثر من ثلاثة من أعضاء المجموعة «س».
نلاحظ في هذه البديهيات السبع، أنه لا يرد فيها ذكر صريح لأية مادة بعينها، فلسنا ندري ماذا تكون المجموعة «س» ولا ماذا تكون فئاتها الفرعية التي تنبثق منها؛ ولا نتطلب فيها إلا رموزًا عامة في دلالاتها.
-
فالكلمات: «مجموعة» و«فئة فرعية» و«أفراد» و«أعضاء»؛ وكذلك أسماء العلاقات: «ينتمي إلى» و«يشتمل على» … إلخ؛ وكذلك فكرة «العدد» مثل «واحد» و«اثنين» و«ثلاثة» كل هذه الكلمات من الجهاز اللفظي الأساسي في علم المنطق، فلسنا في حاجة إلى أي علم آخر ليتاح لنا استخدامها.
-
فلو استطعنا أن نستنتج بعض النتائج من هذه البديهيات لم يكن ذلك بسبب علمنا بأي شيء من أشياء الطبيعة.
-
فهذه المسلمات السبع ليست من قبيل القضايا التي يقال عنها إنها صادقة أو كاذبة، بل هي فروض قدِّمت على أن يُسَلَّم بها؛ ويكفي لبيان ذلك أن نرى أن رموزها الواردة فيها كلها «متغيرات» وليست هي من «الثوابت»٩ فرموز «س» و«أ» و«ب» و«مجموعة» و«فئة فرعية» ليست بذات الدلالة الثابتة، بل تتغير دلالتها بحسب سياقها، فلا اشتراط فيها سوى أن يجيء استعمالها في نسق ما متسقًا مطَّردًا، فيحافظ كل رمز على دلالة واحدة ما دام داخل ذلك النسق، أما إذا استخدم في نسق آخر، فقد يكون له معنى مختلف كل الاختلاف عن معناه في النسق الأول؛ وما دامت الرموز غير ذات قيمة متعينة محددة لها دائمًا مهما كان السياق الذي ترد فيه، فلا تكون الصيغة التي تجيء تلك الرموز جزءًا من بنائها قضية تصدق أو تكذب، بل تكون دالة قضية لا توصف بصدق أو بكذب حتى تحل محل الرموز المجهولة الدلالة رموز أخرى معلومة الدلالة.
فهذه المسلمات السبع — إذن — تصور علاقات قائمة بين أطراف غير مُعَرَّفة، أي إن هذه الأطراف قد تدل على أي شيء نريده لها، ما دامت هذه الدلالة تتمشى مع إطار العلاقات القائمة بينها.
- نظرية ١: إذا كان «أ» و«ب» عضوين متميزين من أعضاء المجموعة «س»،
كانت هناك فئة فرعية واحدة — وواحدة فقط — مشتملة على أ، ب
معًا ويطلق عليها الفئة الفرعية أ ب.
هذه النظرية تلزم مباشرة عن بديهية ١ وبديهية ٢.
- نظرية ٢: أي فئتين فرعيتين متميزتين يكون بينهما عضو واحد — وواحد
فقط — من أعضاء المجموعة «س» مشترك بينهما.
هذه النظرية تلزم عن بديهية ٢ وبديهية ٣.
- نظرية ٣: هناك ثلاثة أعضاء من المجموعة «س» لا تقع كلها في فئة
فرعية واحدة بذاتها.
هذه النظرية نتيجة مباشرة للبديهيات ٤، ٥، ٦.
- نظرية ٤: كل فئة فرعية في المجموعة «س» تشتمل بالضبط على ثلاثة
أعضاء من المجموعة «س».
هذه النظرية تلزم عن بديهية ٥ وبديهية ٧ … إلخ، إلخ.
هذا يبين البناء الرياضي كيف يكون، من حيث هو علم فرضيٌّ استنباطي؛ فالمسلمات الأولى والنظريات المستنتجة منها ليست مستمدة من أية خبرة حسية، وهي وحدها لا تبين إن كان هنالك أو لم يكن في العالم الخارجي مجموعة معينة من أشياء تتفق مع هذا البناء الرياضي فيما بين أفرادها من علاقات.
بناء (٢)
فيما يلي مثل لمجموعة من أفراد وما بينها من علاقات، مما يجوز وجوده في العالم الخارجي؛ فالرموز هنا ليست «متغيرات» ولكنها «ثوابت».
فافرض أن شركة مؤلفة من سبعة شركاء، قرروا أن يكونوا من أنفسهم سبع لجان، لتنظر كل لجنة منها في مجال معين من المجالات التي يشتمل عليها نشاط الشركة؛ ثم اتفقوا كذلك على أن يكون كل عضو منهم رئيسًا لإحدى هذه اللجان، وأن يكون كل عضو منهم مُدْرَجًا في ثلاثة لجان فقط.
فعندئذٍ يكون تقسيم الأسماء على لجان الشركات الفرعية على الوجه الآتي، على فرض أن مجالات النشاط التي تتناولها الشركة هي: النسيج، والنقل، والمباني، والطباعة، والفنادق، وصيد الأسماك، وصناعة الورق، وعلى فرض أن أعضاء الشركة هم، أحمد بكر، وتوفيق، ثروت، حسن، جلال، خالد (والاسم الأول من كل لجنة هو اسم رئيسها).
| النسيج | أحمد | بكر | توفيق |
| النقل | بكر | ثروت | جلال |
| المباني | ثروت | توفيق | حسن |
| الطباعة | توفيق | جلال | خالد |
| الفنادق | جلال | حسن | أحمد |
| صيد الأسماك | حسن | خالد | بكر |
| صناعة الورق | خالد | أحمد | ثروت |
ونظرة تحليلية لهذه القوائم تبين لك أنها تحقق البديهيات السبع الواردة في البناء الرياضي الذي أسلفناه، إذا كنا نفسر «س» بأنها مجموعة الشركاء، ونفسر الفئات الفرعية بأنها اللجان؛ ولنراجع هذه القوائم على تلك البديهيات:
تقول البديهية الأولى إنه إذا كان هنالك مجموعة ما «س» وكانت «أ» و«ب» عضوين في هذه المجموعة، كان هنالك على الأقل فئة فرعية واحدة مشتملة على أ، ب معًا؛ وبترجمة هذه البديهية إلى ما نحن بصدده من أعضاء الشركة، تصبح:
إذا كان أحمد وبكر عضوين متميزين من أعضاء الشركة، فهنالك على الأقل لجنة واحدة مشتملة على أحمد وبكر معًا وكذلك بناءً على البديهية الثانية يكون هنالك على الأكثر لجنة واحدة تضم أحمد وبكر معًا.
وبالجمع بين البديهيتين معًا، يكون هناك لجنة واحدة — وواحدة فقط — من لجان الشركة يجتمع فيها أحمد وبكر معًا.
وهكذا قل في أي عضوين من أعضاء الشركة، فهما لا يجتمعان إلا في لجنة واحدة، وواحدة فقط، فلا أقل من لجنة واحدة، ولا أكثر من لجنة واحدة.
وانتقل إلى البديهية ٣ وطبقها على حالة الشركة التي نحن بصددها فالبديهية تقول: «أي فئتين فرعيتين في المجموعة «س» فيهما على الأقل عضو واحد مشترك بينهما» طبق هذا على حالة الشركة تجد أن أي لجنتين من لجانها لا بد أن يكون فيهما عضو واحد مشترك بينهما؛ وانظر إلى قائمة الأسماء، تجد بكرًا عضوًا مشتركًا بين لجنتين النسيج والنقل، وتجد توفيقًا عضوًا مشتركًا بين لجنتي النسيج والمباني، وتجده أيضًا عضوًا مشتركًا بين النسيج والطباعة … وهكذا مهما تكن اللجنتان تختارهما، تجد بينهما عضوًا مشتركًا.
وتستطيع أن توازن بين بقية البديهيات السبع، وما يلزم عنها من نتائج، وبين الشركة وأعضائها ولجانها، وستجد أن الموازاة تامة بينهما.
بناء (٣)
وسنورد فيما يلي مثلًا آخر، قوامه شكل هندسي ذو خطوط متقاطعة عند نقط بعينها، وسنرى أن شبكة العلاقات التي كانت قائمة في البناء الصوري (١) وقائمة في مثال الشركة الذي رقمناه بالبناء (٢) هي نفسها شبكة العلاقات القائمة في هذا المثال الجديد.
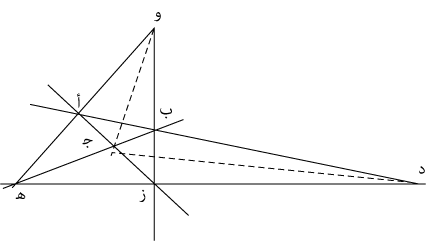
في هذا الشكل سبع نقط هي: أ، ب، ﺟ، د، ﻫ، و، ز تقع ثلاثًا ثلاثًا على سبعة خطوط (أحدها خط منكسر هو الخط المنقوط) وهي: أ د، أ ز، ﻫ د، ﻫ ب، وز، وﺟ د (وهو خط منكسر)، وﻫ فاجعل كل نقطة تمثل عضوًا من أعضاء المجموعة «س» التي ورد ذكرها في البناء الصوري (١)، واجعل كل مجموعة ذات ثلاث نقط واقعة على خط من الخطوط السبعة فئة فرعية، تجد البديهيات السبع متحققة تمامًا كما تحققت في حالة الشركة التي أسلفنا ذكرها.
فبناء على البديهيتين ١، ٢ معًا لا تجتمع أية نقطتين معًا إلا على خط واحد فقط، فلا بد من اجتماعهما على الأقل على خط واحد.
فالنقطتان أ، ب لا تجتمعان إلا على خط واحد هو الخط أ د؛ والنقطتان ﺟ، د لا تجتمعان إلا على خط واحد هو الخط المنكسر وﺟ د، وهكذا.
وبناء على البديهية ٣ تجد أن أي خطين بينهما نقطة مشتركة واحدة، فالخطان أ د، أ ز يشتركان في النقطة أ، وهكذا.
البناء (٤)
وفيما يلي سبعة أعمدة من أعداد، ترى فيها البديهيات المذكورة في البناء الصوري (١) متحققة تمامًا كما تحققت في حالة الشركة ولجانها وأعضائها، وفي حالة الشكل الهندسي ونقطه وخطوطه؛ وأعمدة الأعداد هي:
| ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ |
| ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٠ |
| ٣ | ٤ | ٥ | ٦ | ٠ | ١ | ٢ |
فها هنا أيضًا تجد أن أي عددين مجتمعان في عمود واحد فقط؛ وستجد أيضًا أن أي عمودين تختارهما كما اتفق، يشتملان على عدد واحد فقط مشترك بينهما، وهكذا.
فالبناءات الأربعة السابقة كلها متوازية أو متناظرة أو متشابهة تشابهًا صوريًّا، بمعنى أن بينها علاقة واحد بواحد، فكل عنصر في أحدها يقابله عنصر في الآخر.
فمثلًا:
أحمد في أعضاء الشركة يقابله النقطة أ في الشكل الهندسي، ويقابله أيضًا الصفر في الأعداد.
وبكر في أعضاء الشركة يقابله النقطة ب في الشكل الهندسي، ويقابله أيضًا العدد ١ في مجموعة الأعداد … وهكذا والعلاقة المثلثة الأطراف بين لجنة النسيج في الشركة، وهي اللجنة المؤلفة من أحمد وبكر وتوفيق، يقابلها العلاقة المثلثة الأطراف بين أعداد العمود الأول (في قوائم الأعداد) وهي الأعداد ٠، ١، ٣؛ ويقابلها العلاقة المثلثة الأطراف بين النقط أ، ب، د التي تقع معًا على خط واحد من الشكل الهندسي.
وهذه العلاقات المتناظرة كلها يمكن تجريدها وتعميمها بحيث تصاغ صياغة صورية منطقية هي التي قدمناها في البناء الأول.
ومؤدَّى ذلك كله هو أن البناءات الصورية (في المنطق والرياضة) وإن تكن متحررة من ضرورة ملازمتها لمادة الواقع، إلا أنها قد تجد من مواف الواقع المتجسد ما يتوازى معها طرفًا بطرف وعلاقة بعلاقة.
فإذا كان لدينا صورة رياضية كهذه: «س × ص = ثابت» أي إنه إذا زادت قيمة س نقصت قيمة ص بحيث يظل حاصل ضرب القيمتين ثابتًا دائمًا. فهذه صورة لا مادة يفها، تستطيع أن تجري عليها من التحويلات الصورية النظرية ما يتفق معها؛ لكن ذلك لا يمنع أن نجد من ظواهر الطبيعة ما يوازيها في طريقة التكوين الصوري، فالعلاقة بين حجم الغاز والضغط الواقع عليه تتمثل فيها هذه الصورة نفسها، إذ أن «حجم الغاز × الضغط = ثابت» فلو فرضنا أن حجم الغاز في حالة معينة يساوي تسع أقدام مكعبة، وأن الضغط الواقع عليه يساوي أربعة ضغوط جوية، كان حاصل الضرب الذي هو ٣٦ مقدارًا ثابتًا، بحيث إذا تغير حجم الغاز وأصبح ست أقدام مكعبة، لزم أن يكون الضغط الواقع عليه هو ست ضغوط جوية، لكي يظل حاصل الضرب ٣٦ كما كان في الحالة الأولى.
وربما كانت هذه الصورة الرياضية نفسها هي القالب الصوري الذي ينطبق على علاقة عرض السلعة وثمنها، فربما كان عرض السلعة مضروبًا في ثمنها يساوي مقدارًا ثابتًا، بحيث إذا زاد العرض لزم أن يقل الثمن بحيث يظل حاصل الضرب واحدًا أيضًا.
بهذا تتضح العلاقة بين ما هو صوري خالص من جوانب تفكيرنا، وبين ما هو تجريبي واقع، فعلى الرغم من أن الأول لا يعتمد على الثاني، إلا أنه ضروري لتطوير علمنا بالجانب الثاني تطويرًا سريعًا؛ إذ لولا أننا نطوِّر الفكرة المعينة صوريًّا في أذهاننًا تطويرًا يستخرج منها نتائج قد نجدها نافعة في تحوير العالم الخارجي، لاضطررنا — كما هي الحال عند الحيوان — أن نحور العالم الخارجي تحويرًا فعليًّا دائمًا في كل خطوة نحتاج فيها إلى ذلك، وفي ذلك تضييق شديد لنطاق قدرتنا على التصرف في ظواهر الطبيعة؛ لكننا قد نُجري تحويرات صورية في أذهاننا تعد بالألوف، دون أن نضطر دائمًا إلى التطبيق الفعلي على الطبيعة في كل حالة من هذه الحالات؛ فلا تناقض — إذن — بين أن نقول عن العلوم الصورية من رياضة ومنطق ألا شأن لها بالعالَم الواقع في مادته الفعلية، وبين أن نقول إنها مع ذلك ممكنة التطبيق — عند أي مرحلة شئنا من مراحل سيرها — على ذلك العالَم الواقع.



